题目内容
在极坐标系中,求曲线ρ=2cosθ关于直线θ=
(ρ∈R)对称的曲线的极坐标方程.
| π |
| 4 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:解法一:将极坐标系下的方程转化为直角坐标方程,进一步运算过后再将计算结果表示成极坐标方程.
解法二:在极坐标下,设曲线ρ=2cosθ上任意一点为(ρ′,θ′),其关于直线θ=
对称点为(ρ,θ),则
,再代入到ρ′=2cosθ′计算即可.
解法二:在极坐标下,设曲线ρ=2cosθ上任意一点为(ρ′,θ′),其关于直线θ=
| π |
| 4 |
|
解答:
解法一:以极点为坐标原点,极轴为x轴建立直角坐标系,
则曲线ρ=2cosθ的直角坐标方程为(x-1)2+y2=1,且圆心C为(1,0).
直线θ=
的直角坐标方程为y=x,
因为圆心C(1,0)关于y=x的对称点为(0,1),
所以圆心C关于y=x的对称曲线为x2+(y-1)2=1,
所以曲线ρ=2cosθ关于直线θ=
(ρ∈R)对称的曲线的极坐标方程为ρ=2sinθ.
解法二:设曲线ρ=2cosθ上任意一点为(ρ′,θ′),其关于直线θ=
对称点为(ρ,θ)
则
,
将(ρ′,θ′),代入(ρ′,θ′),得ρ=2cos(
-θ),即ρ=2sinθ,
所以曲线ρ=2cosθ关于直线θ=
对称的曲线的极坐标方程为ρ=2sinθ.
则曲线ρ=2cosθ的直角坐标方程为(x-1)2+y2=1,且圆心C为(1,0).
直线θ=
| π |
| 4 |
因为圆心C(1,0)关于y=x的对称点为(0,1),
所以圆心C关于y=x的对称曲线为x2+(y-1)2=1,
所以曲线ρ=2cosθ关于直线θ=
| π |
| 4 |
解法二:设曲线ρ=2cosθ上任意一点为(ρ′,θ′),其关于直线θ=
| π |
| 4 |
则
|
将(ρ′,θ′),代入(ρ′,θ′),得ρ=2cos(
| π |
| 2 |
所以曲线ρ=2cosθ关于直线θ=
| π |
| 4 |
点评:和极坐标相关的题目可以直接用极坐标的知识处理,也可以根据极坐标和直角坐标的互化转化成直角坐标下的运算,学生可以根据自己的思维方式选择适合的解决方法.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
设变量x,y满足约束条件
,则目标函数z=y-2x的最小值为( )
|
A、-
| ||
| B、-11 | ||
C、-
| ||
| D、3 |
 已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为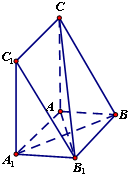 如图,三棱柱ABC-A1B1C1中,∠CAA1=∠A1AB=∠BAC=90°,AB=AA1=1,AC=2.
如图,三棱柱ABC-A1B1C1中,∠CAA1=∠A1AB=∠BAC=90°,AB=AA1=1,AC=2.