题目内容
(Ⅰ)试证明柯西不等式:(a2+b2)(x2+y2)≥(ax+by)2(x,y,a,b∈R)
;(Ⅱ)已知x2+y2=2,且|x|≠|y|,求
+
的最小值.
;(Ⅱ)已知x2+y2=2,且|x|≠|y|,求
| 1 |
| (x+y)2 |
| 1 |
| (x-y)2 |
考点:二维形式的柯西不等式
专题:选作题,不等式
分析:(Ⅰ)利用作差法,即可证明;
(2)令u=x+y,v=x-y,则x=
,y=
,可得u2+v2=4,由柯西不等式得:(
+
)(u2+v2)≥4,即可求得结论.
(2)令u=x+y,v=x-y,则x=
| u+v |
| 2 |
| u-v |
| 2 |
| 1 |
| u2 |
| 1 |
| v2 |
解答:
(Ⅰ)证明:左边=a2x2+a2y2+b2x2+b2y2,右边=a2x2+2abxy+b2y2,
左边-右边=a2y2+b2x2-2abxy=(ay-bx)2≥0,…(2分)
∴左边≥右边,命题得证.…(3分)
(Ⅱ)解:令u=x+y,v=x-y,则x=
,y=
,
∵x2+y2=2,∴(u+v)2+(u-v)2=8,∴u2+v2=4,…(4分)
由柯西不等式得:(
+
)(u2+v2)≥4,…(5分)
当且仅当u=v=
,即x=±
,y=0,或x=,0y=±
时…(6分)
+
的最小值是1.…(7分)
左边-右边=a2y2+b2x2-2abxy=(ay-bx)2≥0,…(2分)
∴左边≥右边,命题得证.…(3分)
(Ⅱ)解:令u=x+y,v=x-y,则x=
| u+v |
| 2 |
| u-v |
| 2 |
∵x2+y2=2,∴(u+v)2+(u-v)2=8,∴u2+v2=4,…(4分)
由柯西不等式得:(
| 1 |
| u2 |
| 1 |
| v2 |
当且仅当u=v=
| 2 |
| 2 |
| 2 |
| 1 |
| (x+y)2 |
| 1 |
| (x-y)2 |
点评:本题考查柯西不等式,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
用数学归纳法证明12+32+52+…+(2n-1)2=
n(4n2-1)过程中,由n=k递推到n=k+1时,不等式左边增加的项为( )
| 1 |
| 3 |
| A、(2k)2 |
| B、(2k+3)2 |
| C、(2k+2)2 |
| D、(2k+1)2 |
 已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为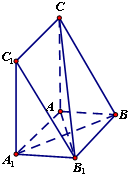 如图,三棱柱ABC-A1B1C1中,∠CAA1=∠A1AB=∠BAC=90°,AB=AA1=1,AC=2.
如图,三棱柱ABC-A1B1C1中,∠CAA1=∠A1AB=∠BAC=90°,AB=AA1=1,AC=2.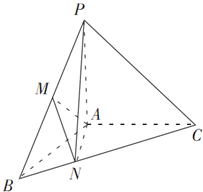 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且AN=
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且AN=