题目内容
已知x∈R,f(x)=
sin2x(
-tan
)+
cos2x.
(1)若0<x<
,求f(x)的单调的递减区间;
(2)若f(x)=
,求x的值.
| 1 |
| 2 |
| 1 | ||
tan
|
| x |
| 2 |
| ||
| 2 |
(1)若0<x<
| π |
| 2 |
(2)若f(x)=
| ||
| 2 |
考点:三角函数中的恒等变换应用,正弦函数的单调性
专题:三角函数的图像与性质
分析:(1)由已知条件化切为弦,利用二倍角公式求出f(x)=sin(2x+
),由此能求出0<x<
时,f(x)的单调的递减区间.
(2)利用正弦函数的性质进行求解.
| π |
| 3 |
| π |
| 2 |
(2)利用正弦函数的性质进行求解.
解答:
解:(1)∵f(x)=
sin2x(
-tan
)+
cos2x,
∴f(x)=
sin2x(
-
)+
cos2x
=
sin2x•
+
cos2x=
sin2x+
cos2x
=sin(2x+
),
∵0<x<
,
∴
≤2x+
<
,
即
≤x<
时,f(x)为减函数,
∴f(x)的递减区间为[
,
).
(2)∵f(x)=sin(2x+
)=
,
∴x=kπ(k∈Z),或x=
+kπ(k∈Z).
| 1 |
| 2 |
| 1 | ||
tan
|
| x |
| 2 |
| ||
| 2 |
∴f(x)=
| 1 |
| 2 |
| 1+cosx |
| sinx |
| 1-cosx |
| sinx |
| ||
| 2 |
=
| 1 |
| 2 |
| 2cosx |
| sinx |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
=sin(2x+
| π |
| 3 |
∵0<x<
| π |
| 2 |
∴
| π |
| 2 |
| π |
| 3 |
| 4π |
| 3 |
即
| π |
| 12 |
| π |
| 2 |
∴f(x)的递减区间为[
| π |
| 12 |
| π |
| 2 |
(2)∵f(x)=sin(2x+
| π |
| 3 |
| ||
| 2 |
∴x=kπ(k∈Z),或x=
| π |
| 6 |
点评:本题考查三角函数的单调减区间的求法,考查给值求角问题,是中档题,解题时要熟练掌握二倍角公式,注意三角函数恒等式的灵活运用.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积为( )


| A、9cm3 | ||
| B、10cm3 | ||
| C、11cm3 | ||
D、
|
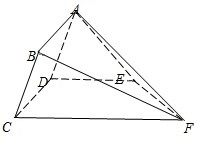 如图,矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角,DE∥CF,CD⊥DE,AD=2,EF=3
如图,矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角,DE∥CF,CD⊥DE,AD=2,EF=3