题目内容
求证:
+
+…+
=
,n∈N*.
| 12 |
| 1•3 |
| 22 |
| 3•5 |
| n2 |
| (2n-1)(2n+1) |
| n(n+1) |
| 2(2n+1) |
考点:数学归纳法
专题:证明题,点列、递归数列与数学归纳法
分析:利用数学归纳法的证明步骤,验证n=1时成立,假设n=k是成立,证明n=k+1时等式也成立即可.
解答:
证明:(1)当n=1时,左边=
,右边=
,等式成立.--(3分)
(2)假设当n=k时,等式成立,即
+
+…+
=
-----(6分)
那么,当n=k+1时,左边=
+
+…+
+
=
+
=
这就是说,当n=k+1时等式也成立.----------------------(13分)
根据(1)和(2),可知等式对任何n∈N*都成立.-----------------------(14分)
| 1 |
| 3 |
| 1 |
| 3 |
(2)假设当n=k时,等式成立,即
| 12 |
| 1•3 |
| 22 |
| 3•5 |
| k2 |
| (2k-1)(2k+1) |
| k(k+1) |
| 2(2k+1) |
那么,当n=k+1时,左边=
| 12 |
| 1•3 |
| 22 |
| 3•5 |
| k2 |
| (2k-1)(2k+1) |
| (k+1)2 |
| (2k+1)(2k+3) |
| k(k+1) |
| 2(2k+1) |
| (k+1)2 |
| (2k+1)(2k+3) |
=
| (k+1)(k+2) |
| 2(2k+3) |
这就是说,当n=k+1时等式也成立.----------------------(13分)
根据(1)和(2),可知等式对任何n∈N*都成立.-----------------------(14分)
点评:本题是中档题,考查数学归纳法的应用,注意数学归纳法证明时,必须用上假设.

练习册系列答案
相关题目
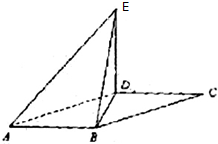 如图,平行四边形ABCD中,∠ABD=90°,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EDB⊥平面ABD.
如图,平行四边形ABCD中,∠ABD=90°,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EDB⊥平面ABD.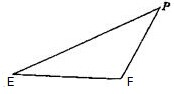 在面积为12的△PEF中,已知tan∠PEF=
在面积为12的△PEF中,已知tan∠PEF=