题目内容
已知向量
=3
-4
,
=6
-3
,
=(5-m)
-(4+m)
,其中
、
分别是直角坐标系内与x轴、y轴方向相同的单位向量.
(1)若A、B、C三点共线,求实数m的值;
(2)若△ABC为直角三角形,且∠A为直角,求实数m的值.
| OA |
| i |
| j |
| OB |
| i |
| j |
| OC |
| i |
| j |
| i |
| j |
(1)若A、B、C三点共线,求实数m的值;
(2)若△ABC为直角三角形,且∠A为直角,求实数m的值.
考点:平面向量数量积的运算
专题:平面向量及应用
分析:(1)利用向量共线定理即可得出;
(2)利用向量垂直与数量积的关系即可得出.
(2)利用向量垂直与数量积的关系即可得出.
解答:
解:(1)
=(3,-4),
=(6,-3),
=(5-m,-4-m),
=
-
=(3,1),
=
-
=(2-m,-m),
∵A、B、C三点共线,
∴存在实数λ使得
=λ
,∴(3,1)=λ(2-m,-m),
,解得m=-1,λ=1.
(2)∵∠A=90°,
∴
⊥
,
∴
•
=3(2-m)+(-m)=0,解得m=
.
| OA |
| OB |
| OC |
| AB |
| OB |
| OA |
| AC |
| OC |
| OA |
∵A、B、C三点共线,
∴存在实数λ使得
| AB |
| AC |
|
(2)∵∠A=90°,
∴
| AB |
| AC |
∴
| AB |
| AC |
| 3 |
| 2 |
点评:本题考查了向量共线定理、向量垂直与数量积的关系,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知定义在R上的函数f(x)关于点(2,0)对称,当x>2时,f(x)单调递增,若x1+x2<4且(x1-2)•(x2-2)<0,则f(x1)+f(x2)值( )
| A、可正可负 | B、可能为0 |
| C、恒大于0 | D、恒小于0 |
将直角坐标方程y=x转化为极坐标方程,可以是( )
| A、ρ=1 | ||
| B、ρ=θ | ||
| C、θ=1 | ||
D、θ=
|
设α是第二象限角,则
是( )
| α |
| 2 |
| A、第一象限角 |
| B、第一或第三象限角 |
| C、第二象限角 |
| D、第一或第二象限角 |
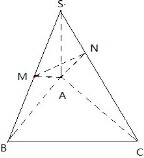 在三棱锥S-ABC中,SA⊥底面ABC,∠ABC=90°,且SA=AB,点M是SB的中点,AN⊥SC且交SC于点N.
在三棱锥S-ABC中,SA⊥底面ABC,∠ABC=90°,且SA=AB,点M是SB的中点,AN⊥SC且交SC于点N.