题目内容
(1)已知双曲线的中心在原点,焦点F1,F2在坐标轴上,离心率为
,且过点(4,-
).求双曲线的标准方程;
(2)已知曲线C上任意一点M到点F(0,1)的距离比它到直线l:y=-2的距离小1.求曲线C的方程.
| 2 |
| 10 |
(2)已知曲线C上任意一点M到点F(0,1)的距离比它到直线l:y=-2的距离小1.求曲线C的方程.
考点:双曲线的标准方程,抛物线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(1)设双曲线方程为x2-y2=λ,由双曲线过点(4,-
),能求出双曲线方程.
(2)由已知得点M的轨迹C是以F为焦点,l′为准线的抛物线,由此能求出曲线C的方程.
| 10 |
(2)由已知得点M的轨迹C是以F为焦点,l′为准线的抛物线,由此能求出曲线C的方程.
解答:
解:(1)∵e=
,
∴可设双曲线方程为x2-y2=λ.
∵双曲线过点(4,-
),
∴16-10=λ,即λ=6.
∴双曲线方程为x2-y2=6.
(2)∵点M到点F(0,1)的距离比它到直线l:y=-2的距离小1,
∴点M在直线l的上方,点M到F(0,1)的距离与它到直线l′:y=-1的距离相等,
∴点M的轨迹C是以F为焦点,l′为准线的抛物线,
∴曲线C的方程为x2=4y.
| 2 |
∴可设双曲线方程为x2-y2=λ.
∵双曲线过点(4,-
| 10 |
∴16-10=λ,即λ=6.
∴双曲线方程为x2-y2=6.
(2)∵点M到点F(0,1)的距离比它到直线l:y=-2的距离小1,
∴点M在直线l的上方,点M到F(0,1)的距离与它到直线l′:y=-1的距离相等,
∴点M的轨迹C是以F为焦点,l′为准线的抛物线,
∴曲线C的方程为x2=4y.
点评:本题考查双曲线方程和曲线方程的求法,是中档题,解题时要注意抛物线和双曲线的简单性质的合理运用.

练习册系列答案
相关题目
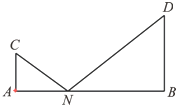 如图,C,D是两个小区的所在地,C,D到一条公路AB的垂直距离CA=1km,DB=2km,AB两端之间的距离为4km.某公交公司将在AB之间找一点N,在N处建造一个公交站台.
如图,C,D是两个小区的所在地,C,D到一条公路AB的垂直距离CA=1km,DB=2km,AB两端之间的距离为4km.某公交公司将在AB之间找一点N,在N处建造一个公交站台.