题目内容
已知函数f(x)=log3(10x+
-2),则f(x)的值域为( )
| 1 |
| 10x |
| A、(-∞,-3) |
| B、(-3,3) |
| C、[0,+∞) |
| D、(-∞,+∞) |
考点:函数的值域
专题:计算题,函数的性质及应用
分析:由基本不等式可得10x+
≥2,从而再由观察法求函数的值域.
| 1 |
| 10x |
解答:
解:∵10x+
≥2,
又∵10x+
-2>0;
∴取10x+
>2即可,
则函数f(x)的值域为R.
故选D.
| 1 |
| 10x |
又∵10x+
| 1 |
| 10x |
∴取10x+
| 1 |
| 10x |
则函数f(x)的值域为R.
故选D.
点评:本题考查了函数值域的求法.高中函数值域求法有:1、观察法,2、配方法,3、反函数法,4、判别式法;5、换元法,6、数形结合法,7、不等式法,8、分离常数法,9、单调性法,10、利用导数求函数的值域,11、最值法,12、构造法,13、比例法.要根据题意选择.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
设两个向量
=(n+2,n-cos2x),
=(m,
+sinx),其中m,n为实数,若存在实数x使得
=2
,则m的取值范围为( )
| a |
| b |
| m |
| 2 |
| a |
| b |
| A、[1,4] |
| B、[0,4] |
| C、[0,2] |
| D、[-6,-2] |
已知i是虚数单位,复数z=
,则|z-2|=( )
| 2i |
| 1+i |
| A、2 | ||
B、2
| ||
C、
| ||
| D、1 |
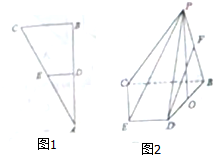 如图1所示,在△ABC中,∠B=90°,D,E分别是AB,AC的中点,将△ADE沿DE折到△PDE的位置,使得∠PDB=60°,如图2所示,连接PB,PC,CD,O,F分别是BD,PB的中点,连接PO,DF,PC.
如图1所示,在△ABC中,∠B=90°,D,E分别是AB,AC的中点,将△ADE沿DE折到△PDE的位置,使得∠PDB=60°,如图2所示,连接PB,PC,CD,O,F分别是BD,PB的中点,连接PO,DF,PC.