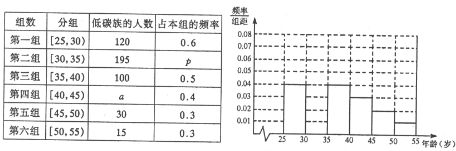
题目内容
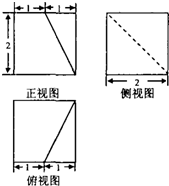
若某几何体的三视图如图所示,则此几何体的体积是( )

A、
| ||
B、
| ||
| C、7 | ||
| D、6 |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由三视图可知:该几何体是一个正方体切去一个三棱锥所得的组合体,分别计算正方体和棱锥的体积,相减可得答案.
解答:
解:由三视图可知:该几何体是一个正方体切去一个三棱锥所得的组合体,如下图:

正方体的体积为:2×2×2=8,
三棱锥的体积为:
×
×1×2×2=
,
故组合体的体积V=8-
=
,
故选:A.

正方体的体积为:2×2×2=8,
三棱锥的体积为:
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
故组合体的体积V=8-
| 2 |
| 3 |
| 22 |
| 3 |
故选:A.
点评:本题考查的知识点由三视图求体积和表面积,其中根据已知中的三视图,判断出几何体的形状,是解答的关键.

练习册系列答案
相关题目
已知i是虚数单位,复数z=
,则|z-2|=( )
| 2i |
| 1+i |
| A、2 | ||
B、2
| ||
C、
| ||
| D、1 |
若非零实数a,b,c成等差数列,则函数y=ax2+bx+
c的图象与x轴交点的个数为( )
| 1 |
| 4 |
| A、0 | B、1 | C、2 | D、1或2 |
 阅读如图所示的程序框图,运行相应的程序.若输出的结果为
阅读如图所示的程序框图,运行相应的程序.若输出的结果为| 1 |
| 2 |
| A、n>3? | B、n<3? |
| C、n<4? | D、n>4? |
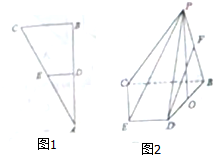 如图1所示,在△ABC中,∠B=90°,D,E分别是AB,AC的中点,将△ADE沿DE折到△PDE的位置,使得∠PDB=60°,如图2所示,连接PB,PC,CD,O,F分别是BD,PB的中点,连接PO,DF,PC.
如图1所示,在△ABC中,∠B=90°,D,E分别是AB,AC的中点,将△ADE沿DE折到△PDE的位置,使得∠PDB=60°,如图2所示,连接PB,PC,CD,O,F分别是BD,PB的中点,连接PO,DF,PC.