题目内容
已知函数f(x)=x2-2acos(k+1)π•lnx(k∈N*,a∈R且a>0).
(1)讨论函数f(x)的单调性;
(2)若k=2015,方程f (x)=2a x有惟一解时,求a的值.
(1)讨论函数f(x)的单调性;
(2)若k=2015,方程f (x)=2a x有惟一解时,求a的值.
考点:利用导数研究函数的单调性,函数的零点,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)求出函数的定义域与导数,通过k是偶数时,k是奇数时,判断导函数的符号,推出函数的单调性即可.(2)通过k=2015,化简f(x)=x2-2alnx(k∈N*),构造g(x)=x2-2axlnx-2ax,求出导数,通过f(x)=2ax有唯一解,转化为g(x)=0有唯一解;通过求解导数函数的极值单调性,然后判断求解a的值.
解答:
(理科)解:(1)由已知得,x>0且f′(x)=2x-(-1)k+1•
.
当k是偶数时,则f′(x)>0,则f(x)在(0,+∞)上是增函数;
当k是奇数时,则 f′(x)=2x-
=
,
所以当x∈(0,
)时,f′(x)<0,当x∈(a,+∞)时,f′(x)>0,
故当k是偶数时,f(x)在(0,
)是减函数,在(a,+∞)是增函数.
(2)若k=2015,则f(x)=x2-2alnx(k∈N*)
记g(x)=f(x)-2ax=x2-2axlnx-2ax,g′(x)=2x-
-2a=
(x2-ax-a),
若方程f(x)=2ax有唯一解,即g(x)=0有唯一解;
令g'(x)=0,得x2-ax-a=0,
∵a>0,x>0∴x 1=
<0(舍去)x 2=
当x∈(0,x2)时,g'(x)<0,g(x)在(0,x2)是单调递减函数;
当x∈(x2,+∞)时,g'(x)>0,g(x)在(x2,+∞)上是单调递增函数.
当x=x2时,g'(x2)=0,g(x)min=g(x2).
∵g(x)=0有唯一解,∴g(x2)=0
则
,即
,
alnx2+ax2-a=0∵a>0,∴2lnx2+x2-1=0(*)
设函数h(x)=2lnx+x-1,
∵在x>0时,h(x)是增函数,∴h(x)=0至多有一解.
∵h(1)=0,∴方程(*)的解为x2=1,即
=1,解得a=
.
| 2a |
| x |
当k是偶数时,则f′(x)>0,则f(x)在(0,+∞)上是增函数;
当k是奇数时,则 f′(x)=2x-
| 2a |
| x |
2(x+
| ||||
| x |
所以当x∈(0,
| a |
故当k是偶数时,f(x)在(0,
| a |
(2)若k=2015,则f(x)=x2-2alnx(k∈N*)
记g(x)=f(x)-2ax=x2-2axlnx-2ax,g′(x)=2x-
| 2a |
| x |
| 2 |
| x |
若方程f(x)=2ax有唯一解,即g(x)=0有唯一解;
令g'(x)=0,得x2-ax-a=0,
∵a>0,x>0∴x 1=
a-
| ||
| 2 |
a+
| ||
| 2 |
当x∈(0,x2)时,g'(x)<0,g(x)在(0,x2)是单调递减函数;
当x∈(x2,+∞)时,g'(x)>0,g(x)在(x2,+∞)上是单调递增函数.
当x=x2时,g'(x2)=0,g(x)min=g(x2).
∵g(x)=0有唯一解,∴g(x2)=0
则
|
|
alnx2+ax2-a=0∵a>0,∴2lnx2+x2-1=0(*)
设函数h(x)=2lnx+x-1,
∵在x>0时,h(x)是增函数,∴h(x)=0至多有一解.
∵h(1)=0,∴方程(*)的解为x2=1,即
a+
| ||
| 2 |
| 1 |
| 2 |
点评:本题考查函数的导数求解函数的单调性以及函数的极值,函数的零点个数,构造法的应用,考查分析问题解决问题的能力.

练习册系列答案
相关题目


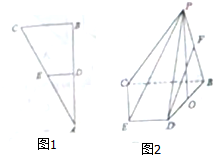 如图1所示,在△ABC中,∠B=90°,D,E分别是AB,AC的中点,将△ADE沿DE折到△PDE的位置,使得∠PDB=60°,如图2所示,连接PB,PC,CD,O,F分别是BD,PB的中点,连接PO,DF,PC.
如图1所示,在△ABC中,∠B=90°,D,E分别是AB,AC的中点,将△ADE沿DE折到△PDE的位置,使得∠PDB=60°,如图2所示,连接PB,PC,CD,O,F分别是BD,PB的中点,连接PO,DF,PC.