题目内容
已知全集U=R，集合A={x||x-1|≤2}，CUB=（-∞，1）∪[4，+∞），则A∪B=（ ）
| A、[1，3] |
| B、（1，3] |
| C、[-1，4] |
| D、[-1，4） |
考点：并集及其运算
专题：集合
分析：先分别求出集合A和集合B，然后再求出集合A∪B．
解答：
解：∵CUB=（-∞，1）∪[4，+∞），
∴B={x|1≤x＜4}，
又∵集合A={x||x-1|≤2}={x|-1≤x≤3}，
∴A∪B={x|-1≤x≤3}∪{x|1≤x＜4}={x|-1≤x＜4}．
故选：D．
∴B={x|1≤x＜4}，
又∵集合A={x||x-1|≤2}={x|-1≤x≤3}，
∴A∪B={x|-1≤x≤3}∪{x|1≤x＜4}={x|-1≤x＜4}．
故选：D．
点评：本题考查集合的性质和运算，解题时要根据实际情况，注意公式的灵活运用．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
设两个向量
=（n+2，n-cos2x），
=（m，
+sinx），其中m，n为实数，若存在实数x使得
=2
，则m的取值范围为（ ）
| a |
| b |
| m |
| 2 |
| a |
| b |
| A、[1，4] |
| B、[0，4] |
| C、[0，2] |
| D、[-6，-2] |
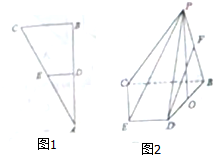如图1所示，在△ABC中，∠B=90°，D，E分别是AB，AC的中点，将△ADE沿DE折到△PDE的位置，使得∠PDB=60°，如图2所示，连接PB，PC，CD，O，F分别是BD，PB的中点，连接PO，DF，PC．设集合A={{x|y=
}，集合B={x||x-2|＜2}，则A∩B等于（ ）
| 2+x-x2 |
| A、（0，2] | B、[0，2] |
| C、[-1，2） | D、∅ |
已知i是虚数单位，复数z=
，则|z-2|=（ ）
| 2i |
| 1+i |
| A、2 | ||
B、2
| ||
C、
| ||
| D、1 |
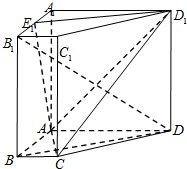如图，在四棱柱ABCD-A1B1C1D1中，侧棱AA1⊥底面 ABCD，底面ABCD是直角梯形，AD∥BC，∠BAD=90°，AD=AA1=3，BC=1，E1为A1B1中点．