题目内容
若x4(x+3)8=a0+a1(x+2)+a2(x+2)2+…+a12(x+2)12,则log2(a1+a3+…+a11)= .
考点:二项式系数的性质
专题:二项式定理
分析:只需令x=-4与x=-1,得到的两个表达式解方程组,即可求出a1+a3+a5+…+a11的值,然后求出结果.
解答:
解:当x=-1时,x+2=1.等式化为:(-1)4•28=1=a0+a1+a2+…+a12.
∴a0+a1+a2+…+a12=256…①
当x=-3时,x+2=-1.等式化为:(-3)4•08=0=a0-a1+a2-a3+…+a12…②
上述①②两等式相相减有:a1+a3+…+a11=
(256+0)=128,
log2(a1+a3+…+a11)=log2128=7.
故答案为:7.
∴a0+a1+a2+…+a12=256…①
当x=-3时,x+2=-1.等式化为:(-3)4•08=0=a0-a1+a2-a3+…+a12…②
上述①②两等式相相减有:a1+a3+…+a11=
| 1 |
| 2 |
log2(a1+a3+…+a11)=log2128=7.
故答案为:7.
点评:本题考查二项式定理的应用,赋值法是解答二项式定理系数的问题的有效途径之一.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
某工厂甲、乙、丙三个车间生产同一产品,数量分别为120件,90件,60件.为了解它们的产品质量是否有显著差异,用分层抽样方法抽取了一个容量为n的样本进行调查,其中从丙车间的产品中抽取了4件,则n= .
已知直线l1:x+ky-2k=0与l2:kx-(k-2)y+1=0垂直,则k的值是( )
| A、1 | B、3 | C、1或-2 | D、0或3 |
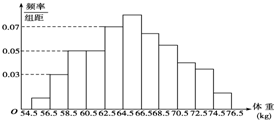 为了解某地区高三学生的身体发育情况,抽查了该地区100名高三男生的体重.根据抽样测量后的男生体重(单位:kg)数据绘制的频率分布直方图如图所示,则这100名学生中体重值在区间[56.5,64.5)的人数是
为了解某地区高三学生的身体发育情况,抽查了该地区100名高三男生的体重.根据抽样测量后的男生体重(单位:kg)数据绘制的频率分布直方图如图所示,则这100名学生中体重值在区间[56.5,64.5)的人数是