题目内容
某工厂甲、乙、丙三个车间生产同一产品，数量分别为120件，90件，60件．为了解它们的产品质量是否有显著差异，用分层抽样方法抽取了一个容量为n的样本进行调查，其中从丙车间的产品中抽取了4件，则n= ．
考点：分层抽样方法
专题：概率与统计
分析：根据从丙车间的产品中抽取的个数可得分层抽样的抽取比例，再由总体个数乘以抽取比例可得样本容量．
解答：
解：由从丙车间的产品中抽取了4件得分层抽样的抽取比例为
=
．
又总体个数为120+90+60=270，
∴样本容量n=270×
=18．
故答案为：18．
| 4 |
| 60 |
| 1 |
| 15 |
又总体个数为120+90+60=270，
∴样本容量n=270×
| 1 |
| 15 |
故答案为：18．
点评：本题考查了分层抽样方法，熟练掌握分层抽样的定义是关键．
练习册系列答案
阅读快车系列答案
相关题目
已知一个样本容量为100的样本数据的频率分布直方图如图所示，样本数据落在[40，60）内的频数为设f（x）=2x+x-4，则函数f（x）的零点位于区间（ ）
| A、（-1，0） |
| B、（0，1） |
| C、（1，2） |
| D、（2，3） |
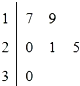某车间共有6名工人，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数，日加工零件个数大于样本均值的工人为优秀工人．从该车间6名工人中，任取2人，则恰有1名优秀工人的概率为（ ）