题目内容

已知函数f（x）满足f（x）=
f(x+1)  (x＜2)
(
1
2
)x   (x≥2)
，求f（log23）的值．
考点：函数的值
专题：函数的性质及应用
分析：根据函数的表达式直接代入即可得到结论．
解答： 解：∵1＜log23＜2，
∴2＜log23+1＜3，
∴f（log23）=f（log23+1）=f（log26）=(
1
2
)log26=2-log26=2log2
1
6
=
1
6
．
点评：本题主要考查函数值的计算，根据条件直接代入即可，比较基础．
练习册系列答案
相关题目
定义函数f（x）={x．{x}}，其中{x}表示不小于x的最小整数，如{1.4）=2，{-2.3}=-2．当x∈（0，n]（n∈N*）时，函数f（x）的值域为An，记集合An中元素的个数为an，则
lim
n→∞
（
1
a1
+
1
a2
+…+
1
an
）=
 
．
设函数y=f（x）的定义域为D，若对于任意x1、x2∈D，当x1+x2=2a时，恒有f（x1）+f（x2）=2b，则称点（a，b）为函数y=f（x）图象的对称中心．研究函数f（x）=x+sinπx-3的某一个对称中心，并利用对称中心的上述定义，可得到f（
1
2014
）+f（
2
2014
）+…+f（
4026
2014
 ）+f（
4027
2014
）的值为（　　）
A、4027B、-4027
C、8054D、-8054
已知a=log23，b=8-0.4，c=sin
12
5
π，则a，b，c的大小关系是（　　）
A、a＞b＞c
B、a＞c＞b
C、b＞a＞c
D、c＞b＞a
平面直角坐标系xoy中，已知点（n，an）（n∈N*）在函数y=ax（a≥2，a∈N）的图象上，点（n，bn）（n∈N*）在直线y=（a+1）x+b（b∈R）上．
（1）若点（1，a1）与点（1，b1）重合，且a2＜b2，求数列{bn}的通项公式；
（2）证明：当a=2时，数列{an}中任意三项都不能构成等差数列；
（3）当b=1时，记A={x|x=an，n∈N*}，B={x|x=bn，n∈N*}，设C=A∩B，将集合C的元素按从小到大的顺序排列组成数列{cn}，写出数列{cn}的通项公式cn．
要建一个容积为200m3，深为2m的长方体无盖水池，池壁的造价为80元/m2，池底的造价为120元/m2，设水池的底面长为x（单位：m），其造价为y（单位：元），
（1）求总造价y关于底面长x的函数解析式y=f（x）；
（2）求f（x）的最小值．
已知圆心为C的圆经过点A（1，1）和B（2，-2），且圆心在直线l：x-y+1=0上．
（1）求圆心为C的圆的标准方程；
（2）点P是圆C上的任一点，求当点P到直线x+y-5=0的距离最小时，P点的坐标．
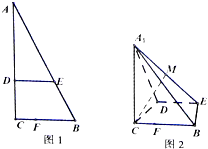如图1，在Rt△ABC中，∠C=90°，BC=3，AC=6，D，E，F分别是AC，AB CB上的点，且DE∥BC，DE=2，CF=1，将△ADE沿DE折起到△A1DE的位置，使AC⊥CD，如图2．
（1）求证：A1C⊥平面BCDE；
（2）若M是A1E的中点，求CM与平面A1BE所成角的正弦值；
（3）试问线段A1C上是否存在点P，使平面FDP∥平面A1BE？请你说明理由．
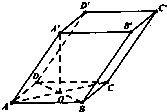如图四棱柱ABCD-A′B′C′D′的底面是正方形，O是底面的中心，A′O=1，AB=AA′=A′D=A′B=
2
．
（1）证明：平面A′BD∥平面B′CD′；
（2）求二面角A-BC-B′的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网