题目内容
定义在R上的函数f(x)满足f(x+2)=f(x)+1,且x∈[0,1]时,f(x)=4x,x∈(1,2)时,f(x)=
,令g(x)=2f(x)-x-4x∈[-6,2],则函数g(x)的零点个数为( )
| f(1) |
| x |
| A、9 | B、8 | C、7 | D、6 |
考点:抽象函数及其应用
专题:函数的性质及应用
分析:由x∈[0,1]时,f(x)=4x,可得f(1)=4,x∈(1,2)时,f(x)=
=
,而由函数f(x)满足f(x+2)=f(x)+1,即自变量x每增加2个单位,函数图象向上平移1个单位,自变量每减少2个单位,函数图象向下平移1个单位,画出函数图象,结合函数的图象可求.
| f(1) |
| x |
| 4 |
| x |
解答:
解:∵x∈[0,1]时,f(x)=4x,
∴f(1)=4
∴x∈(1,2)时,f(x)=
=
,
∵g(x)=2f(x)-x-4,x∈[-6,2],
令g(x)=2f(x)-x-4=0,
即f(x)=
x+2
∵函数f(x)满足f(x+2)=f(x)+1,即自变量x每增加2个单位,函数图象向上平移1个单位,自变量每减少2个单位,函数图象向下平移1个单位,
分别画出函数y=f(x)在x∈[-6,2],y=
x+2的图象,
∴y=f(x)在x∈[-6,2],y=
x+2有8个交点,
故函数g(x)的零点个数为8个.

故选:B.
∴f(1)=4
∴x∈(1,2)时,f(x)=
| f(1) |
| x |
| 4 |
| x |
∵g(x)=2f(x)-x-4,x∈[-6,2],
令g(x)=2f(x)-x-4=0,
即f(x)=
| 1 |
| 2 |
∵函数f(x)满足f(x+2)=f(x)+1,即自变量x每增加2个单位,函数图象向上平移1个单位,自变量每减少2个单位,函数图象向下平移1个单位,
分别画出函数y=f(x)在x∈[-6,2],y=
| 1 |
| 2 |
∴y=f(x)在x∈[-6,2],y=
| 1 |
| 2 |
故函数g(x)的零点个数为8个.

故选:B.
点评:本题考查的知识点是对数函数的图象与性质,利用转化思想,将函数的零点个数问题,转化为函数图象交点个数问题,是解答本题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
已知直线AB与抛物线y2=2x交于A,B两点,M是AB的中点,C是抛物线上的点,且使得
•
取最小值,抛物线在点C处的切线为l,则( )
| CA |
| CB |
| A、CM⊥AB | ||
| B、CM⊥l | ||
| C、CA⊥CB | ||
D、CM=
|
函数f(x)=xsinx+cosx的导函数原点处的部分图象大致为( )
A、 |
B、 |
C、 |
D、 |
下列函数可用二分法求其在区间(0,1)内零点的是( )
A、y=
| |||||||||||
| B、y=4x2-4x+1 | |||||||||||
C、y=ln
| |||||||||||
D、y=
|
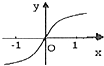
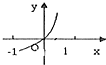
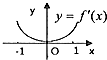 已知函数y=f(x)的导函数y=f′(x)的图象如图所示,则下列选项中能表示函数y=f(x)图象的是( )
已知函数y=f(x)的导函数y=f′(x)的图象如图所示,则下列选项中能表示函数y=f(x)图象的是( )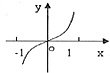
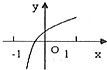
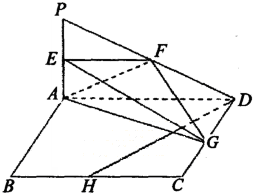 如图,四边形ABCD为正方形,PA⊥平面ABCD,且AD=2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.
如图,四边形ABCD为正方形,PA⊥平面ABCD,且AD=2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.