题目内容
下列函数可用二分法求其在区间(0,1)内零点的是( )
A、y=
| |||||||||||
| B、y=4x2-4x+1 | |||||||||||
C、y=ln
| |||||||||||
D、y=
|
考点:二分法求方程的近似解
专题:函数的性质及应用
分析:根据二分法的定义,函数必须是连续函数,且函数在零点两侧的函数值异号,从而可得结论.
解答:
解:f(x)=
的图象在区间(0,1)内是连续的,且f(0)•f(1)<0,故可用二分法求其在区间(0,1)内零点,
f(x)=4x2-4x+1的图象在区间(0,1)内是连续的,但f(0)•f(1)>0,故不可用二分法求其在区间(0,1)内零点,
f(x)=ln
-x3的图象在区间(0,1)内是连续的,但f(0)•f(1)>0,故不可用二分法求其在区间(0,1)内零点,
f(x)=
-
的图象在区间(0,1)内是不连续的,故不可用二分法求其在区间(0,1)内零点,
故选:A
|
f(x)=4x2-4x+1的图象在区间(0,1)内是连续的,但f(0)•f(1)>0,故不可用二分法求其在区间(0,1)内零点,
f(x)=ln
| 2-x |
| 3 |
f(x)=
| 1 |
| 2x-1 |
| 1 |
| 3 |
故选:A
点评:本题考查二分法的定义,理解函数必须是连续函数,且函数在零点两侧的函数值异号,属于基础题.

练习册系列答案
相关题目
定义在R上的函数f(x)满足f(x+2)=f(x)+1,且x∈[0,1]时,f(x)=4x,x∈(1,2)时,f(x)=
,令g(x)=2f(x)-x-4x∈[-6,2],则函数g(x)的零点个数为( )
| f(1) |
| x |
| A、9 | B、8 | C、7 | D、6 |
用二分法求方程3x+3x-8=0在区间(1,2)的过程中,设函数f(x)=3x+3x-8,算得f(1)<0,f(1.25)<0,f(1.5)>0,f(1.75)>0,则该方程的根属于( )
| A、(1,1.25) |
| B、(1.25,1.5) |
| C、(1.5,1.75) |
| D、(1.75,2) |
已知等差数列{an}的前n项和为Sn,若
=a1
+a20
,且A、B、C三点共线(该直线不过点O),则S20=( )
| OB |
| OA |
| OC |
| A、10 | B、11 | C、20 | D、21 |
如果0<x<1,0<y<1,那么关于0<
<1( )
| x |
| y |
| A、正确 | B、错误 | C、不确定 |
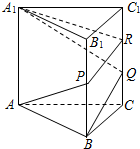 已知正三棱柱ABC-A1B1C1的底面边长与侧棱长相等.蚂蚁甲从A点沿表面经过棱BB1,CC1爬到点A1,蚂蚁乙从B点沿表面经过棱CC1爬到点A1.如图,设∠PAB=α,∠QBC=β,若两只蚂蚁各自爬过的路程最短,则α+β=
已知正三棱柱ABC-A1B1C1的底面边长与侧棱长相等.蚂蚁甲从A点沿表面经过棱BB1,CC1爬到点A1,蚂蚁乙从B点沿表面经过棱CC1爬到点A1.如图,设∠PAB=α,∠QBC=β,若两只蚂蚁各自爬过的路程最短,则α+β=