题目内容
设函数f(x)=
的定义域为集合A,函数g(x)=lg(
-1)的定义域为集合B,已知p:x∈A∩B;q:x满足2x+m<0,且若p则q为真命题,求实数m的取值范围.
| x2-x-2 |
| 3 |
| x |
考点:复合命题的真假
专题:简易逻辑
分析:本题的关键是求解设函数f(x)=
的定义域为集合A,函数g(x)=lg(
-1)的定义域为集合B,在利用p:x∈A∩B;q:x满足2x+m<0,求解m的取值范围
| x2-x-2 |
| 3 |
| x |
解答:
解:∵函数f(x)=
的定义域为集合A
∴A={x|x2-x-2≥0}={x|x≤-1或x≥2},
∵函数g(x)=lg(
-1)的定义域为集合B
∴B={x|
-1>0}={x|0<x<3},
∴A∩B={x|2≤x<3}
记C={x|2x+m<0}={x|x<-
}
又∵若p则q为真命题,即p⇒q
∴A∩B⊆C
∴3≤-
,即m≤-6
综上,实数m的取值范围为{m|m≤-6}
| x2-x-2 |
∴A={x|x2-x-2≥0}={x|x≤-1或x≥2},
∵函数g(x)=lg(
| 3 |
| x |
∴B={x|
| 3 |
| x |
∴A∩B={x|2≤x<3}
记C={x|2x+m<0}={x|x<-
| m |
| 2 |
又∵若p则q为真命题,即p⇒q
∴A∩B⊆C
∴3≤-
| m |
| 2 |
综上,实数m的取值范围为{m|m≤-6}
点评:本题考查的知识点是复合命题的真假判定,解决的办法是先判断组成复合命题的简单命题的真假,再根据真值表进行判断.

练习册系列答案
相关题目
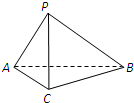 如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC. 如图所示,在长方体ABCD-A1B1C1D1中,AA1=2,AB=AD=1,点M是CC1的中点,
如图所示,在长方体ABCD-A1B1C1D1中,AA1=2,AB=AD=1,点M是CC1的中点,