题目内容
已知(x2-
)n的展开式中含x的项为第6项,且(1-x+2x2)n=a0+a1x+a2x2+…+a2nx2n,
(1)求n的值;
(2)求a1+a2+…+a2n的值.
| 1 |
| x |
(1)求n的值;
(2)求a1+a2+…+a2n的值.
考点:二项式系数的性质
专题:二项式定理
分析:(1)求得(x2-
)n的展开式的通项公式为Tr+1=(-1)r•
•x2n-3r,根据当r=5时,x的幂指数等于1,求得n的值.
(2)在 (1-x+2x2)n=a0+a1x+a2x2+…+a2nx2n 中,令x=0,可得a0=1.再令x=1可得,2n=28=1+a1+a2+…+a2n ,从而求得a1+a2+…+a2n,的值.
| 1 |
| x |
| C | r n |
(2)在 (1-x+2x2)n=a0+a1x+a2x2+…+a2nx2n 中,令x=0,可得a0=1.再令x=1可得,2n=28=1+a1+a2+…+a2n ,从而求得a1+a2+…+a2n,的值.
解答:
解:(1)∵已知(x2-
)n的展开式中含x的项为第6项,
而它的通项公式为Tr+1=
•x2n-2r•(-1)r•x-r=(-1)r•
•x2n-3r,
∴当r=5时,2n-3r=1,n=8.
(2)∵(1-x+2x2)n=a0+a1x+a2x2+…+a2nx2n,令x=0,可得a0=1.
令x=1可得,2n=28=1+a1+a2+…+a2n ,∴a1+a2+…+a2n,=28-1=255.
| 1 |
| x |
而它的通项公式为Tr+1=
| C | r n |
| C | r n |
∴当r=5时,2n-3r=1,n=8.
(2)∵(1-x+2x2)n=a0+a1x+a2x2+…+a2nx2n,令x=0,可得a0=1.
令x=1可得,2n=28=1+a1+a2+…+a2n ,∴a1+a2+…+a2n,=28-1=255.
点评:本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若双曲线
-
=1(a>0,b>0)的右顶点为A,过其左焦点F作x轴的垂线交双曲线于M,N两点,且
•
>0,则该双曲线离心率的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
| MA |
| NA |
| A、(2,+∞) | ||
| B、(1,2) | ||
C、(
| ||
D、(1,
|
 如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,且DM=2
如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,且DM=2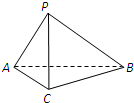 如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC. 如图所示,在长方体ABCD-A1B1C1D1中,AA1=2,AB=AD=1,点M是CC1的中点,
如图所示,在长方体ABCD-A1B1C1D1中,AA1=2,AB=AD=1,点M是CC1的中点,