题目内容
设a为实数,函数f(x)=x|x-6a|+|a|x+b.
(1)若f(x)为奇函数,求a,b的值;
(2)若b=1,试讨论方程f(x)=0的零点情况.
(1)若f(x)为奇函数,求a,b的值;
(2)若b=1,试讨论方程f(x)=0的零点情况.
考点:函数的零点
专题:计算题,函数的性质及应用
分析:(1)由f(x)=x|x-6a|+|a|x+b为奇函数知f(0)=b=0,f(1)+f(-1)=|1-6a|+|a|-|-1-6a|-|a|=0,从而解得;
(2)由题意,f(x)=x|x-6a|+|a|x+1,讨论去绝对值号,从而讨论方程的根的个数.
(2)由题意,f(x)=x|x-6a|+|a|x+1,讨论去绝对值号,从而讨论方程的根的个数.
解答:
解:(1)∵f(x)=x|x-6a|+|a|x+b为奇函数,
∴f(0)=b=0;
f(1)+f(-1)=|1-6a|+|a|-|-1-6a|-|a|=0,
解得,a=0;
故f(x)=x|x|,
经检验为奇函数;
(2)由题意,f(x)=x|x-6a|+|a|x+1,
当a=0时,f(x)=x|x|+1=0,
解得,x=-1;
当a>0时,
f(x)=x|x-6a|+ax+1=0;
可化为x2-7ax-1=0;
方程的负根是x|x-6a|+ax+1=0的根;
当a<0时,f(x)=x|x-6a|-ax+1=0可化为x2-7ax+1=0(x>6a);
当△=0,即a=-
时,x=-1;
当△>0,即a<-
时,
当6a•6a-7a•6a+1>0,即-
<a<-
时,有两个解,
当6a•6a-7a•6a+1≤0,即a≤-
时,有一个解;
也可化为x2-5ax-1=0(x≤6a);
6a•6a-5a•6a-1≤0,-
≤a<0时,有一个解,
当6a•6a-5a•6a-1>0,-
>a时,无解,
综上所述,当a≥-
时,方程有一个解,
当a=-
时方程有2个解,
当-
<a<-
时方程有3个解,
当a=-
时有两个解,
当a<-
时有1个解.
∴f(0)=b=0;
f(1)+f(-1)=|1-6a|+|a|-|-1-6a|-|a|=0,
解得,a=0;
故f(x)=x|x|,
经检验为奇函数;
(2)由题意,f(x)=x|x-6a|+|a|x+1,
当a=0时,f(x)=x|x|+1=0,
解得,x=-1;
当a>0时,
f(x)=x|x-6a|+ax+1=0;
可化为x2-7ax-1=0;
方程的负根是x|x-6a|+ax+1=0的根;
当a<0时,f(x)=x|x-6a|-ax+1=0可化为x2-7ax+1=0(x>6a);
当△=0,即a=-
| 2 |
| 7 |
当△>0,即a<-
| 2 |
| 7 |
当6a•6a-7a•6a+1>0,即-
| ||
| 6 |
| 2 |
| 7 |
当6a•6a-7a•6a+1≤0,即a≤-
| ||
| 6 |
也可化为x2-5ax-1=0(x≤6a);
6a•6a-5a•6a-1≤0,-
| ||
| 6 |
当6a•6a-5a•6a-1>0,-
| ||
| 6 |
综上所述,当a≥-
| 2 |
| 7 |
当a=-
| 2 |
| 7 |
当-
| ||
| 6 |
| 2 |
| 7 |
当a=-
| ||
| 6 |
当a<-
| ||
| 6 |
点评:本题考查了函数的性质应用,属于基础题.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
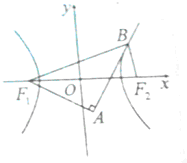 如图,F1,F2分别是双曲线
如图,F1,F2分别是双曲线