题目内容
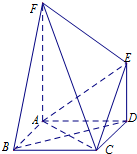 如图所示的几何体中,直线AF⊥平面ABCD,且ABCD为正方形,ADEF为梯形,DE∥AF,又AB=1,AF=2DE=2a.
如图所示的几何体中,直线AF⊥平面ABCD,且ABCD为正方形,ADEF为梯形,DE∥AF,又AB=1,AF=2DE=2a.(Ⅰ)求证:直线CE∥平面ABF;
(Ⅱ)求证:直线BD⊥平面ACF;
(Ⅲ)若直线AE⊥CF,求a的值.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(I)由AB∥CD,DE∥AF,且AB∩AF=A,CD∩DE=D,可证平面ABF∥平面DCE即可证明CE∥平面ABF.
(II) 先证明AC⊥BD,AF⊥BD,即可证明直线BD⊥平面ACF.
(Ⅲ) 连接 FD,易证明CD⊥AE.又AE⊥CF,可证AE⊥FD.从而可得∠EAD+∠FDA=
,即有tan∠EAD=
=
=
,即可解得a的值.
(II) 先证明AC⊥BD,AF⊥BD,即可证明直线BD⊥平面ACF.
(Ⅲ) 连接 FD,易证明CD⊥AE.又AE⊥CF,可证AE⊥FD.从而可得∠EAD+∠FDA=
| π |
| 2 |
| a |
| 1 |
| 1 |
| tan∠EAD |
| 1 |
| 2a |
解答:
(本小题满分12分)
解:( I)因为ABCD为正方形,所以AB∥CD.-------------(1分)
又DE∥AF,且AB∩AF=A,CD∩DE=D.
所以平面ABF∥平面DCE.-------------(3分)
而CE?平面EDC,
所以CE∥平面ABF.-------------(4分)
(II) 因为ABCD为正方形,所以AC⊥BD-------------(5分)
因为直线AF⊥平面ABCD,
所以AF⊥BD,-------------(6分)
因为AF∩AC=A,
所以直线BD⊥平面ACF.-------------(8分)
(Ⅲ) 连接 FD.

因为直线AF⊥平面ABCD,
所以AF⊥CD,
又CD⊥AD,AD∩AF=A
所以CD⊥平面ADEF,-------------(9分)
所以CD⊥AE.
又AE⊥CF,FC∩CD=C,
所以AE⊥平面FCD,
所以AE⊥FD.-------------(11分)
所以∠EAD+∠FDA=
,
所以tan∠EAD=
=
=
解得a=
.-------------(12分).
解:( I)因为ABCD为正方形,所以AB∥CD.-------------(1分)
又DE∥AF,且AB∩AF=A,CD∩DE=D.
所以平面ABF∥平面DCE.-------------(3分)
而CE?平面EDC,
所以CE∥平面ABF.-------------(4分)
(II) 因为ABCD为正方形,所以AC⊥BD-------------(5分)
因为直线AF⊥平面ABCD,
所以AF⊥BD,-------------(6分)
因为AF∩AC=A,
所以直线BD⊥平面ACF.-------------(8分)
(Ⅲ) 连接 FD.

因为直线AF⊥平面ABCD,
所以AF⊥CD,
又CD⊥AD,AD∩AF=A
所以CD⊥平面ADEF,-------------(9分)
所以CD⊥AE.
又AE⊥CF,FC∩CD=C,
所以AE⊥平面FCD,
所以AE⊥FD.-------------(11分)
所以∠EAD+∠FDA=
| π |
| 2 |
所以tan∠EAD=
| a |
| 1 |
| 1 |
| tan∠FDA |
| 1 |
| 2a |
解得a=
| ||
| 2 |
点评:本题主要考察了直线与平面垂直的判定,直线与平面平行的判定,考察了转化思想,属于中档题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
探照灯反射镜的轴截面是抛物线y2=2px(x>0)的一部分,光源位于抛物线的焦点处,已知灯口圆的直径为60cm,灯深40cm,则抛物线的焦点坐标为( )
A、(
| ||
B、(
| ||
C、(
| ||
D、(
|
若点A(-3,-4),B(6,3)到直线l:ax+y+1=0的距离相等,则实数a的值为( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知函数f(x)=
其中a∈R,若对任意的非零实数x1,存在唯一的非零实数x2(x1≠x2),使得f(x1)=f(x2)成立,则k的最大值为( )
|
| A、-1 | B、-2 | C、-4 | D、-3 |
函数f(x)=ln|x-2|-m(m∈R)的所有零点之和为( )
| A、-4 | B、2 |
| C、4 | D、与实数m有关 |