题目内容
在△ABC中,三个内角A,B,C的对边分别是a,b,c,且
=
.
(1)求角B;
(2)若a+c=3
,S△ABC=
,求b的值.
| cosA |
| cosB |
| 2c-a |
| b |
(1)求角B;
(2)若a+c=3
| 3 |
3
| ||
| 2 |
考点:余弦定理,正弦定理
专题:解三角形
分析:(1)由
=
,利用正弦定理可得
=
,化为sin(A+B)=sinC=2sinCcosB,cosB=
,即可解出.
(2)由S△ABC=
=
acsinB=
acsin
,可得ac=6,再利用余弦定理即可得出.
| cosA |
| cosB |
| 2c-a |
| b |
| cosA |
| cosB |
| 2sinC-sinA |
| sinB |
| 1 |
| 2 |
(2)由S△ABC=
3
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
解答:
解:(1)∵
=
,由正弦定理可得
=
,
化为sinAcosB+cosAsinB=2sinCcosB,
∴sin(A+B)=sinC=2sinCcosB,
∵sinC≠0,
∴cosB=
,
∵B∈(0,π),
∴B=
.
(2)∵S△ABC=
=
acsinB=
acsin
,∴ac=6,
又a+c=3
,
∴b2=a2+c2-2accosB=(a+c)2-2ac-2accos
=(3
)2-3×6=9,
解得b=3.
| cosA |
| cosB |
| 2c-a |
| b |
| cosA |
| cosB |
| 2sinC-sinA |
| sinB |
化为sinAcosB+cosAsinB=2sinCcosB,
∴sin(A+B)=sinC=2sinCcosB,
∵sinC≠0,
∴cosB=
| 1 |
| 2 |
∵B∈(0,π),
∴B=
| π |
| 3 |
(2)∵S△ABC=
3
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
又a+c=3
| 3 |
∴b2=a2+c2-2accosB=(a+c)2-2ac-2accos
| π |
| 3 |
| 3 |
解得b=3.
点评:本题考查了正弦定理、余弦定理的应用、三角形的面积计算公式、两角和差的正弦余弦公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某几何体的三视图如图所示,则t=x-y的取值范围是( )
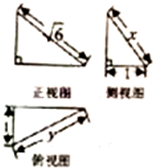

| A、[-4,4] | ||||
| B、(-1,1) | ||||
| C、[-1,1] | ||||
D、(1-
|
一个正三棱柱恰好有一个内切球(球与三棱柱的两个底面和三个侧面都相切)和一个外接球(球经过三棱柱的6个顶点),则此内切球与外接球表面积之比为( )
| A、1:3 | B、1:5 |
| C、1:7 | D、1:9 |
执行程序框图,输出的结果为( )


| A、9 | B、8 | C、6 | D、4 |
已知an=-2n2+9n+3,则数列{an}中的最大项为( )
| A、a1=10 |
| B、a2=13 |
| C、a3=12 |
| D、以上均不正确 |