题目内容
已知函数f（x）=
，当x≠0时，f（
）等于 ．
| 1 |
| 1-x |
| 1 |
| f(x) |
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：根据函数f（x）的解析式，求出
，再求f（
）．
| 1 |
| f(x) |
| 1 |
| f(x) |
解答：
解：∵函数f（x）=
，
∴
=1-x，
∴当x≠0时，f（
）=f（1-x）=
=
．
故答案为：
．
| 1 |
| 1-x |
∴
| 1 |
| f(x) |
∴当x≠0时，f（
| 1 |
| f(x) |
| 1 |
| 1-(1-x) |
| 1 |
| x |
故答案为：
| 1 |
| x |
点评：本题考查了根据函数的解析式求函数值的应用问题，是基础题目．
练习册系列答案
全能测控期末小状元系列答案
相关题目
设集合P={x|y=
+1}，Q={y|y=x3}，则P∩Q=（ ）
| x |
| A、∅ | B、[0，+∞） |
| C、（0，+∞） | D、[1，+∞） |
2014年巴西世界杯刚结束，某足球协会为了调查球迷对本届世界杯的了解情况，组织了“世界杯你问我答一百问”活动，该协会从参加活动的球迷（人数不少于1000人）中随机抽取12名球迷．进行世界杯知识问卷测试，测试成绩（百分制）以茎叶图形式表示如右图所示，根据主办方标准．测试成绩低于80分的为“伪球迷”，不低于80分的为“真球迷”．若某算法框图如图所示，则输出的结果为（ ）
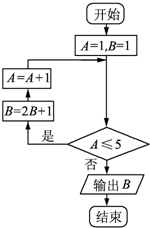
| A、7 | B、15 | C、31 | D、63 |
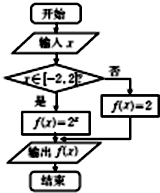阅读如图所示的程序框图，如果输出的函数值在区间[| 1 |
| 4 |
| 1 |
| 2 |
| A、[-2，-1] |
| B、（-∞，-1] |
| C、[-1，2] |
| D、[2，+∞） |
已知命题p：“x＞3”是“x2＞9”的充要条件，命题q：“?x0∈R，x0-2＞0”的否定是“?x0∈R，x0-2＜0”（ ）
| A、“p∨q”为真 |
| B、“p∧q”为真 |
| C、p真q假 |
| D、p，q均为假 |