题目内容
求y=
-
x+
的最小值.
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 9+x2 |
考点:函数的最值及其几何意义
专题:计算题,函数的性质及应用,导数的综合应用
分析:求导y′=-
+
=
;再令f(x)=2x-
,从而求导f′(x)=2-
=
>0;从而由导数的正负确定函数的单调性,从而求最值.
| 1 |
| 2 |
| x | ||
|
2x-
| ||
2
|
| 9+x2 |
| x | ||
|
2
| ||
|
解答:
解:∵y=
-
x+
,
∴y′=-
+
=
;
令f(x)=2x-
,
则f′(x)=2-
=
>0;
故f(x)=2x-
在R上是增函数,
令2x-
=0得,x=
;
故当x∈(-∞,
)时,y′<0;
当x∈(
,+∞)时,y′>0;
故当x=
时,y=
-
x+
取得最小值为
ymin=
-
+
=3
.
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 9+x2 |
∴y′=-
| 1 |
| 2 |
| x | ||
|
2x-
| ||
2
|
令f(x)=2x-
| 9+x2 |
则f′(x)=2-
| x | ||
|
2
| ||
|
故f(x)=2x-
| 9+x2 |
令2x-
| 9+x2 |
| 3 |
故当x∈(-∞,
| 3 |
当x∈(
| 3 |
故当x=
| 3 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 9+x2 |
ymin=
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 9+3 |
| 3 |
点评:本题考查了导数的综合应用,属于中档题.

练习册系列答案
相关题目
已知cos(60°+α)=
,且α为第三象限角,则cos(30°-α)+sin(30°-α)的值为( )
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
命题“若函数f(x)=logax(a>0,a≠1)在其定义域内是减函数,则loga2<0”的逆否命题是( )
| A、若loga2<0,则函数f(x)=logax(a>0,a≠1)在其定义域内不是减函数 |
| B、若loga2≥0,则函数f(x)=logax(a>0,a≠1)在其定义域内不是减函数 |
| C、若loga2<0,则函数f(x)=logax(a>0,a≠1)在其定义域内是减函数 |
| D、若loga2≥0,则函数f(x)=logax(a>0,a≠1)在其定义域内是减函数 |
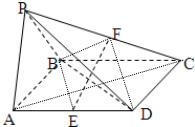 已知四棱锥P-ABCD是底面为平行四边形,面PAB⊥面ABCD,△PAB为正三角形,且AB=
已知四棱锥P-ABCD是底面为平行四边形,面PAB⊥面ABCD,△PAB为正三角形,且AB=