题目内容
3.定义在R上的偶函数f(x),当0≤x≤$\frac{π}{2}$时,f(x)=x3sinx,设a=f(sin$\frac{π}{3}$),b=f(sin2),c=f(sin3),则a,b,c的大小关系为( )| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | c<b<a |
分析 由题意可得,定义在R上的偶函数f(x),当0≤x≤$\frac{π}{2}$时,f(x)=x3sinx是增函数,再由sin2=sin(π-2),sin3=sin(π-3),$π-3<\frac{π}{3}<π-2$,利用函数的单调性可得a,b,c的大小关系.
解答 解:定义在R上的偶函数f(x),当0≤x≤$\frac{π}{2}$时,f(x)=x3sinx是增函数.
由于sin2=sin(π-2),sin3=sin(π-3),$π-3<\frac{π}{3}<π-2$,
∴sin(π-3)<sin$\frac{π}{3}$<sin(π-2),
∴b>a>c,
故选C.
点评 本题主要考查函数的奇偶性和单调性的应用,诱导公式,属于中档题.

练习册系列答案
相关题目
14.函数f(x)=$\frac{3}{sinx+2}$的值域为( )
| A. | (1,3) | B. | (1,3] | C. | [1,3) | D. | [1,3] |
11.四棱柱ABCD-A1B1C1D1中,∠A1AB=∠A1AD=∠DAB=60°,A1A=AB=AD,则CC1与BD所成角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
15.以x轴为对称轴,以原点为顶点且过圆x2+y2-2x+6y+9=0的圆心的抛物线的方程是( )
| A. | y=3x2或y=-3x2 | B. | y=3x2 | C. | y2=-9x或y=3x2 | D. | y2=9x |
12.若|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=1,且($\sqrt{3}$$\overrightarrow{a}$+$\overrightarrow{b}$)$•\overrightarrow{b}$=-2,则cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=( )
| A. | -$\frac{\sqrt{6}}{3}$ | B. | -$\frac{1}{3}$ | C. | -$\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
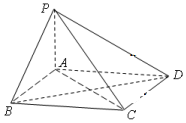 如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD
如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD