题目内容
11.四棱柱ABCD-A1B1C1D1中,∠A1AB=∠A1AD=∠DAB=60°,A1A=AB=AD,则CC1与BD所成角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
分析 由已知推导出CC1∥BB1,从而∠DBB1是CC1与BD所成角(或所成角的补角),由已知得$\overrightarrow{D{B}_{1}}$=$\overrightarrow{DA}+\overrightarrow{AB}+\overrightarrow{B{B}_{1}}$,设A1A=AB=AD=1,则BD=1,求出DB1=$\sqrt{2}$,由此能求出CC1与BD所成角.
解答 解: 四棱柱ABCD-A1B1C1D1中,
四棱柱ABCD-A1B1C1D1中,
∵∠A1AB=∠A1AD=∠DAB=60°,A1A=AB=AD,
$\overrightarrow{D{B}_{1}}$=$\overrightarrow{DA}+\overrightarrow{AB}+\overrightarrow{B{B}_{1}}$,
∴CC1∥BB1,∴∠DBB1是CC1与BD所成角(或所成角的补角),
设A1A=AB=AD=1,则BD=1,
$\overrightarrow{D{B}_{1}}$2=${\overrightarrow{DA}}^{2}+{\overrightarrow{AB}}^{2}+\overrightarrow{B{{B}_{1}}^{2}}$+2|$\overrightarrow{DA}$|•|$\overrightarrow{AB}$|cos120°+2|$\overrightarrow{DA}$|•|$\overrightarrow{B{B}_{1}}$|cos120°+2|$\overrightarrow{AB}$|•|$\overrightarrow{B{B}_{1}}$|cos60°
=1+1+1-1-1+1=2,
∴DB1=$\sqrt{2}$,
∴$D{B}^{2}+B{{B}_{1}}^{2}=D{{B}_{1}}^{2}$,
∴∠DBB1=90°,
∴CC1与BD所成角为90°.
故选:D.
点评 本题考查两条异面直线所成角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

 名校课堂系列答案
名校课堂系列答案| A. | (a,-f(a)) | B. | (a,-f(-a)) | C. | (-a,-f(a)) | D. | (-a,f(a)) |
| A. | (1,+∞) | B. | [1,+∞) | C. | (2,+∞) | D. | [2,+∞) |
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | c<b<a |
| A. | 2 | B. | 3 | C. | 4 | D. | $\frac{11}{2}$ |
| A. | {x|x<1} | B. | {x|x>1} | C. | {x|x<-1或x>1} | D. | {x|x<-1或0<x<1} |
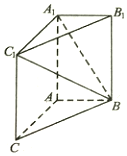 如图,在三棱柱ABC-A1B1C1中,平面ABC⊥平面AA1B1B,四边形AA1B1B是矩形,且AB=1,AC=2,BC=$\sqrt{5}$.
如图,在三棱柱ABC-A1B1C1中,平面ABC⊥平面AA1B1B,四边形AA1B1B是矩形,且AB=1,AC=2,BC=$\sqrt{5}$.