题目内容
18.已知正实数x,y满足xy(x+3y)=x-2y,那么y的最大值为1.分析 根据题意,将xy(x+3y)=x-2y变形可得yx2+(3y2-1)x+2y=0,原问题可以转化为方程yx2+(3y2-1)x+2y=0有正数根的问题,结合二次函数的性质可得$\left\{\begin{array}{l}{△=(3{y}^{2}-1)^{2}-8{y}^{2}≥0}\\{-\frac{3{y}^{2}-1}{2y}>0}\end{array}\right.$,解可得y的取值范围,即可得答案.
解答 解:根据题意,由xy(x+3y)=x-2y,变形可得yx2+(3y2-1)x+2y=0,
而x、y都是正实数,
则方程yx2+(3y2-1)x+2y=0有正数根,
又由$\frac{c}{a}$=2>0,则方程yx2+(3y2-1)x+2y=0的两根同号,
则有$\left\{\begin{array}{l}{△=(3{y}^{2}-1)^{2}-8{y}^{2}≥0}\\{-\frac{3{y}^{2}-1}{2y}>0}\end{array}\right.$,
解可得y2≤$\frac{7-2\sqrt{10}}{6}$,
即0<y≤$\frac{\sqrt{5}-\sqrt{2}}{3}$,
即y的最大值为$\frac{\sqrt{5}-\sqrt{2}}{3}$.
点评 本题考查不等式的应用,关键是将不等式转化为方程有正数解的问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.在如图所示的计算1+5+9+…+2013的程序框图中,判断框内应填入( )
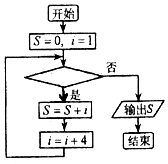

| A. | i≤504 | B. | i≤2009 | C. | i≤2013 | D. | i<2013 |
9.已知复数z满足(z-1)i=i+1,则z在复平面内所对应的点在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
6.已知α∈($\frac{3}{2}$π,2π),且满足cos(α+$\frac{2017}{2}$π)=$\frac{3}{5}$,则sinα+cosα=( )
| A. | -$\frac{7}{5}$ | B. | -$\frac{1}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{7}{5}$ |
10.已知p:${log_2}({{x^2}-3x})>2$,q:$\frac{x-4}{x+1}>0$,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7. 一个几何体的三视图如右图所示,则该几何体的体积为( )
一个几何体的三视图如右图所示,则该几何体的体积为( )
 一个几何体的三视图如右图所示,则该几何体的体积为( )
一个几何体的三视图如右图所示,则该几何体的体积为( )| A. | $\frac{5}{3}$ | B. | $\frac{{10\sqrt{3}}}{3}$ | C. | $\frac{10}{3}$ | D. | $\frac{{5\sqrt{3}}}{3}$ |
 如图,四边形ABCD是边长为1的正方形,ED⊥平面ABCD,FB∥ED,且ED=FB=1,G为BC的中点.
如图,四边形ABCD是边长为1的正方形,ED⊥平面ABCD,FB∥ED,且ED=FB=1,G为BC的中点.