题目内容
一个边长为1的正方形，是一水平放置的一个平面图形的直观图，则原图的周长为（ ）
| A、8 | ||
| B、6 | ||
C、2（1+
| ||
D、2（1+
|
考点：平面图形的直观图
专题：空间位置关系与距离
分析：由斜二测画法的规则知在已知图形平行于x轴的线段，在直观图中画成平行于x'轴，长度保持不变，已知图形平行于y轴的线段，在直观图中画成平行于y'轴，且长度为原来一半．由于y'轴上的线段长度为
，故在平面图中，其长度为2
，且其在平面图中的y轴上，由此可以求得原图形的周长．
| 2 |
| 2 |
解答：
解：由斜二测画法的规则知与x'轴平行的线段其长度不变以及与横轴平行的性质不变，
正方形的对角线在y'轴上，
可求得其长度为
，
故在平面图中其在y轴上，且其长度变为原来的2倍，长度为2
，
其原来的图形如图所示，
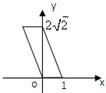
则原图形的两边长分别为1和3，
故原图形的周长是：8．
故选：A
正方形的对角线在y'轴上，
可求得其长度为
| 2 |
故在平面图中其在y轴上，且其长度变为原来的2倍，长度为2
| 2 |
其原来的图形如图所示，
则原图形的两边长分别为1和3，
故原图形的周长是：8．
故选：A
点评：本题考查的知识点是平面图形的直观图，其中斜二测画法的规则，能够帮助我们快速的在直观图面积和原图面积之间进行转化．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
已知m，n是两条直线，α，β是两个平面，有以下命题：
①m，n相交且都在平面α，β外，m∥α，m∥β，n∥α，n∥β，则α∥β；
②若m∥α，m∥β，则α∥β；
③若m∥α，n∥β，m∥n，则α∥β．
其中正确命题的个数是（ ）
①m，n相交且都在平面α，β外，m∥α，m∥β，n∥α，n∥β，则α∥β；
②若m∥α，m∥β，则α∥β；
③若m∥α，n∥β，m∥n，则α∥β．
其中正确命题的个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
在△ABC中，|
|=3，|
|=2，点D满足2
=3
，∠BAC=60°，则
•
=（ ）
| AB |
| AC |
| BD |
| DC |
| AD |
| BC |
A、-
| ||
B、
| ||
C、
| ||
D、-
|