题目内容
设函数f（x）满足f（x）=1+f（
）log3x，则f（3）= ．
| 1 |
| 3 |
考点：函数的值
专题：函数的性质及应用
分析：由已知得f（3）=1+f（
）log33=1+f（
），令x=
，得f（
）=1+f（
）log3
=1-f（
），由此能求出f（3）．
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
解答：
解：∵f（x）=1+f（
）log3x，
∴f（3）=1+f（
）log33=1+f（
），
令x=
，得f（
）=1+f（
）log3
=1-f（
），
解得f(
)=
，
∴f（3）=1+f（
）=1+
=
．
故答案为：
．
| 1 |
| 3 |
∴f（3）=1+f（
| 1 |
| 3 |
| 1 |
| 3 |
令x=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
解得f(
| 1 |
| 3 |
| 1 |
| 2 |
∴f（3）=1+f（
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
故答案为：
| 3 |
| 2 |
点评：本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
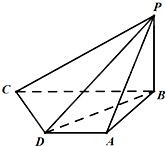如图所示，已知四棱锥P-ABCD中，底面ABCD是直角梯形，AD∥BC，AB⊥BC，AB=AD=1，BC=2，PB⊥平面ABCD，PB=1．一个边长为1的正方形，是一水平放置的一个平面图形的直观图，则原图的周长为（ ）
| A、8 | ||
| B、6 | ||
C、2（1+
| ||
D、2（1+
|
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，且PB与底面ABCD所成的角为45°，E为PB的中点，过A，E，D三点的平面记为α，PC与α的交点为Q．