题目内容

在△ABC中，|
AB
|=3，|
AC
|=2，点D满足2
BD
=3
DC
，∠BAC=60°，则
AD
•
BC
=（　　）
A、-
8
5
B、
9
5
C、
8
5
D、-
9
5
考点：平面向量数量积的运算
专题：平面向量及应用
分析：首先，根据余弦定理，得|BC|2=7，然后根据2
BD
=3
DC
，得到
BD
=
3
5
BC
，再借助于数量积的概念求解即可．
解答： 解：在△ABC中，|
AB
|=3，|
AC
|=2，∠BAC=60°，
根据余弦定理，得
|BC|2=|AB|2+|AC|2-2||AB||AC|cos60°=7，
∵2
BD
=3
DC
，
∴
BD
=
3
5
BC
，
∵
AD
=
AB
+
BD
=
AB
+
3
5
BC

∴
BC
•
AD
=
BC
•
AB
+
3
5
|
BC
|2
=（
AC
-
AB
）•
AB
+
3
5
×7
=|
AC
||
AB
|cos60°-|
AB
|2+
21
5

=2×3×
1
2
-9+
21
5

=-
9
5

则
BC
•
AD
=-
9
5
．
故选：D．
点评：本题重点考查了平面向量的基本运算、向量共线的条件、平面向量基本定理等知识，属于中档题．
练习册系列答案
相关题目
已知全集U=Z，集合A={0，1}，B={-1，0，1，2}，则如图中阴影部分所表示的集合为
 
．
函数y=lnx在区间（0，1）上是
 
函数．
一个边长为1的正方形，是一水平放置的一个平面图形的直观图，则原图的周长为（　　）
A、8
B、6
C、2（1+
3
）
D、2（1+
2
）
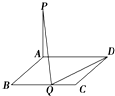如图，在矩形ABCD中，AB=1，BC=a（a＞0），PA⊥平面AC，BC边上存在点Q，使得PQ⊥QD，则实数a的取值范围是
 
．
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，且PB与底面ABCD所成的角为45°，E为PB的中点，过A，E，D三点的平面记为α，PC与α的交点为Q．
（Ⅰ）试确定Q的位置并证明；
（Ⅱ）求四棱锥P-ABCD被平面α分成上下两部分的体积比．
（Ⅲ）若PA=2，截面AEQD的面积为3，求平面α与平面PCD所成的二面角的正切值．
在锐角△ABC中，若2sinB=
3
b，a=1，则∠A=
 
．
设函数f（x）=2cosxcos（x-
π
6
）-sinx（
3
sinx-cosx）+2．
（1）求f（x）的最小正周期；
（2）当x∈[0，
π
2
]时，求f（x）的最大值，单调区间．
（3）若f（x）的图象向x轴正方向平移m个单位后图象关于y轴对称，求m的最小值．
若双曲线x2-
y2
m
=1的一个焦点与抛物线y2=8x的焦点重合，则此双曲线的渐近线方程为（　　）
A、x±y=0
B、
3
x±y=0
C、
5
x±y=0
D、
15
x±y=0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网