题目内容
7.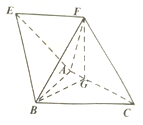 如图,在四棱锥A-EFCB中,四边形EFCB是梯形,EF∥BC且EF=$\frac{3}{4}$BC,△ABC是边长为2的正三角形,顶点F在AC上射影为点G,且FG=$\sqrt{3}$,CF=$\frac{{\sqrt{21}}}{2}$,BF=$\frac{5}{2}$.
如图,在四棱锥A-EFCB中,四边形EFCB是梯形,EF∥BC且EF=$\frac{3}{4}$BC,△ABC是边长为2的正三角形,顶点F在AC上射影为点G,且FG=$\sqrt{3}$,CF=$\frac{{\sqrt{21}}}{2}$,BF=$\frac{5}{2}$.(1)证明:平面FGB⊥平面ABC;
(2)求三棱锥E-GBC的体积.
分析 (1)由顶点F在AC上投影为点G,得FG⊥AC.取AC的中点为O,连结OB,GB,推导出FG⊥BG,从而FG⊥面ABC,由此能证明面FGB⊥面ABC.
(Ⅱ)由VE-GBC=VF-GBC,能求出三棱锥E-GBC的体积.
解答 证明:(1)由顶点F在AC上投影为点G,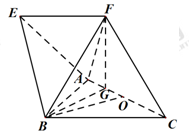
可知,FG⊥AC.
取AC的中点为O,连结OB,GB.
在Rt△FGC中,$FG=\sqrt{3}$,$CF=\frac{{\sqrt{21}}}{2}$,所以$CG=\frac{3}{2}$.
在Rt△GBO中,$OB=\sqrt{3}$,$OG=\frac{1}{2}$,所以$BG=\frac{{\sqrt{13}}}{2}$.
∴BG2+GF2=FB2,即FG⊥BG.
∵FG⊥AC,FG⊥GB,AC∩BG=G
∴FG⊥面ABC.
又FG⊆面FGB,∴面FGB⊥面ABC.
解:(Ⅱ)∵EF∥BC,EF?面ABC,BC⊆面ABC
∴EF∥面ABC.VE-GBC=VF-GBC
∴三棱锥E-GBC的体积${V_{E-GBC}}={V_{F-GBC}}=\frac{1}{3}×{S_{△GBC}}×h=\frac{1}{3}×\frac{{3\sqrt{3}}}{4}×\sqrt{3}=\frac{3}{4}$.
点评 本题考查面面垂直的证明,考查三棱锥的体积的求法,涉及到空间中线线、线面、面面间的位置关系等知识点,考查推理论证能力、运算求解能力、数据处理能力,考查化归与转化思想、函数与方程思想、数形结合思想,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知复数z=x+(x-a)i,若对任意实数x∈(1,2),恒有|z|>|$\overline{z}$+i|,则实数a的取值范围为( )
| A. | (-∞,$\frac{1}{2}$] | B. | (-∞,$\frac{1}{2}$) | C. | [$\frac{3}{2}$,+∞) | D. | ($\frac{3}{2}$,+∞) |
15.已知数列{an}是等比数列,a3=1,a5=4,则公比q等于( )
| A. | 2 | B. | -2 | C. | $±\frac{1}{2}$ | D. | ±2 |
2.在抛物线y=x2与直线y=2围成的封闭图形内任取一点A,O为坐标原点,则直线OA被该封闭图形解得的线段长小于$\sqrt{2}$的概率是( )
| A. | $\frac{{\sqrt{3}}}{15}$ | B. | $\frac{{\sqrt{3}}}{16}$ | C. | $\frac{{\sqrt{2}}}{16}$ | D. | $\frac{{\sqrt{2}}}{14}$ |
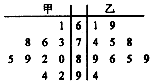 甲、乙两位同学参加数学竞赛培训,培训期间共参加了10次模拟考试,根据考试成绩,得到如图所示的茎叶图.
甲、乙两位同学参加数学竞赛培训,培训期间共参加了10次模拟考试,根据考试成绩,得到如图所示的茎叶图.