题目内容
9．
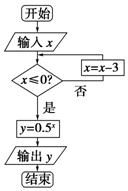如图所示的程序框图，当输入x的值为3时，则其输出的结果是1．
分析 当输入x的值为3时，x=3-3=0，由x=0≤0成立，能求出结果．
解答 解：当输入x的值为3时，
第一次循环时，x=3-3=0，
∵x=0≤0成立，
∴y=0.50=1．
输出y=1．
故答案为：1．
点评 本题主要考查了当型循环结构，循环结构有两种形式：当型循环结构和直到型循环结构，当型循环是先判断后循环，直到型循环是先循环后判断，属于基础题．
练习册系列答案
期末100分闯关海淀考王系列答案
相关题目
4．有这样一段演绎推理：“指数函数y=ax（a＞0且a≠1）是增函数，而y=（$\frac{1}{2}$）x是指数函数，所以y=（$\frac{1}{2}$）x是增函数”．上面推理显然是错误的，是因为（ ）
| A． | 大前提错导致结论错 | B． | 小前提错导致结论错 | ||
| C． | 推理形式错导致结论错 | D． | 大前提和小前提错导致结论错 |
20．
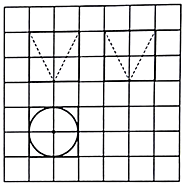如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的表面积为（ ）
如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的表面积为（ ）| A． | $20+\sqrt{5}π$ | B． | $24+\sqrt{5}π$ | C． | $20+（\sqrt{5}-1）π$ | D． | $24+（\sqrt{5}-1）π$ |
17．已知复数z=x+（x-a）i，若对任意实数x∈（1，2），恒有|z|＞|$\overline{z}$+i|，则实数a的取值范围为（ ）
| A． | （-∞，$\frac{1}{2}$] | B． | （-∞，$\frac{1}{2}$） | C． | [$\frac{3}{2}$，+∞） | D． | （$\frac{3}{2}$，+∞） |
14．通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：
其中${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
附表
问能否有99%以上的把握认为爱好该项运动与性别有关？
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
附表
| P（K2≥k） | 0.050 | 0.010 | 0.001 |
| k | 3，841 | 6.635 | 10.828 |
1．已知函数$f（x）=\left\{\begin{array}{l}-2x-{x^2}，x≤0\\|{lgx}|，x＞0\end{array}\right.$，若a＜b＜c＜d，且f（a）=f（b）=f（c）=f（d），则a+b+c+2d的取值范围是（ ）
| A． | $（{3，\frac{201}{10}}）$ | B． | $（{1，\frac{181}{10}}）$ | C． | $（{2\sqrt{2}，+∞}）$ | D． | $（{2\sqrt{2}-2，+∞}）$ |
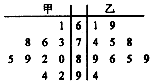甲、乙两位同学参加数学竞赛培训，培训期间共参加了10次模拟考试，根据考试成绩，得到如图所示的茎叶图．