Question

9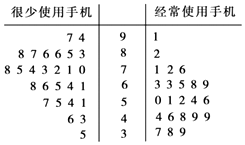．当今信息时代，众多中小学生也配上了手机．某机构为研究经常使用手机是否对学习成绩有影响，在某校高三年级50名理科生第人的10次数学考成绩中随机抽取一次成绩，用茎叶图表示如图：
（Ⅰ）根据茎叶图中的数据完成下面的2×2列联表，并判断是否有95%的把握认为经常使用手机对学习成绩有影响？

	及格（60及60以上）	不及格	合计
很少使用手机	20	7	27
经常使用手机	10	13	23
合计	30	20	50

（Ⅱ）从50人中，选取一名很少使用手机的同学（记为甲）和一名经常使用手机的同学（记为乙）解一道函数题，甲、乙独立解决此题的概率分别为P₁，P₂，P₂=0.4，若P₁-P₂≥0.3，则此二人适合为学习上互帮互助的“对子”，记X为两人中解决此题的人数，若E（X）=1.12，问两人是否适合结为“对子”？
参考公式及数据：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$，其中n=a+b+c+d

P（K2≥k0）	0.10	0.05	0.025
k0	2.706	3.841	5.024

Answer 1

分析 （I）由题意计算对应数据，填写列联表，由联列表中数据计算K²，对照临界值得出结论；
（II）依题意知X的可能取值，写出X的分布列，计算数学期望，求出P₁的值，从而得出结论．

解答 解：（I）由题意得列联表为

	及格	不及格	合计
很少使用手机	20	7	27
经常使用手机	10	13	23
合计	30	20	50

由联列表可得：${K^2}=\frac{{50{{（{20×13-10×7}）}^2}}}{30×20×27×23}≈4.84＞3.841$，
所以有95%的把握认为经常使用手机对学习有影响；
（II）依题意：解决此题的人数X的可能取值为0，1，2，
可得X的分布列为

X	0	1	2
P	（1-P1）（1-P2）	（1-P1）P1+P2（1-P2）	P1•P2

数学期望为E（X）=P₁+P₂=1.12，∴P₁=1.12-0.4=0.72，
∴P₁-P₂=0.32≥0.3，
所以二人适合结为“对子”．

点评 本题考查了独立性检验与离散型随机变量的分布列和数学期望的应用问题，是中档题．