题目内容
13.在△ABC中,角A,B,C所对应的边分别为a,b,c,a-b=bcosC.(1)求证:sinC=tanB;
(2)若a=1,b=2,求c.
分析 (1)由正弦定理可知a-b=bcosC,则sinA-sinB=sinBcosC,由A=π-(B+C),根据诱导公式及两角和的正弦公式,即可求得sinC=tanB;
(2)由题意求得$cosC=-\frac{1}{2}$,利用余弦定理即可求得c的值.
解答 解:(1)由正弦定理可知:$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R,则a=2RsinA,b=2RsinB,c=2RsinC,
由a-b=bcosC,则sinA-sinB=sinBcosC,
由A=π-(B+C),则sinA=sin[π-(B+C)]=sin(B+C),
即sin(B+C)=sinB+sinBcosC,sinBcosC+cosBsinC=sinB+sinBcosC,
sinCcosB=sinB,tanB=$\frac{sinB}{cosB}$,
∴sinC=tanB.
(Ⅱ)由a-b=bcosC,且a=1,b=2,得$cosC=-\frac{1}{2}$,
由余弦定理,${c^2}={a^2}+{b^2}-2abcosC=1+4-2×1×2×({-\frac{1}{2}})=7$,
∴$c=\sqrt{7}$,
c的值为$\sqrt{7}$.
点评 本题考查正弦定理及余弦定理的应用,两角和的正弦公式,考查计算能力,属于基础题.

练习册系列答案
相关题目
9.某校高二年级共有2000人,其中男生1100人,女生900人,为调查该年级学生每周平均体育运动时间的情况,采用分成抽样的方法抽取200人进行分析,统计的数据如表(时间单位:小时).
男、女运动时间情况的调查表:
(Ⅰ)计算x,y的值,根据以上统计数据完成下面的每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该级部学生的每周平均体育运动时间与性别有关”.
附:
(Ⅱ)在每周平均体育运动时间在8小时以上的被调查的人中,喜欢乒乓球的有6人,其中男生4人,女生2人;级部决定从这4名男省中选2人,2名女生中选1人,组成代表队参加校运动会,则男生A和女生E恰好都被选中的概率是多少?
男、女运动时间情况的调查表:
| 时间 | (0,2) | [2,4) | [4,6) | [6,8) | 8小时以上 |
| 男生人数 | 10 | 25 | 35 | 30 | x |
| 女生人数 | 15 | 30 | 25 | y | 5 |
| 男生 | 女生 | 总计 | |
| 平均时间不超过6小时 | |||
| 平均时间超过6小时 | |||
| 总计 |
| K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$ | P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 6.635 | 7.789 |
9.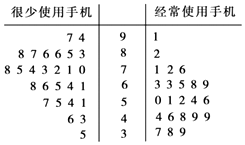 当今信息时代,众多中小学生也配上了手机.某机构为研究经常使用手机是否对学习成绩有影响,在某校高三年级50名理科生第人的10次数学考成绩中随机抽取一次成绩,用茎叶图表示如图:
当今信息时代,众多中小学生也配上了手机.某机构为研究经常使用手机是否对学习成绩有影响,在某校高三年级50名理科生第人的10次数学考成绩中随机抽取一次成绩,用茎叶图表示如图:
(Ⅰ)根据茎叶图中的数据完成下面的2×2列联表,并判断是否有95%的把握认为经常使用手机对学习成绩有影响?
(Ⅱ)从50人中,选取一名很少使用手机的同学(记为甲)和一名经常使用手机的同学(记为乙)解一道函数题,甲、乙独立解决此题的概率分别为P1,P2,P2=0.4,若P1-P2≥0.3,则此二人适合为学习上互帮互助的“对子”,记X为两人中解决此题的人数,若E(X)=1.12,问两人是否适合结为“对子”?
参考公式及数据:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d
 当今信息时代,众多中小学生也配上了手机.某机构为研究经常使用手机是否对学习成绩有影响,在某校高三年级50名理科生第人的10次数学考成绩中随机抽取一次成绩,用茎叶图表示如图:
当今信息时代,众多中小学生也配上了手机.某机构为研究经常使用手机是否对学习成绩有影响,在某校高三年级50名理科生第人的10次数学考成绩中随机抽取一次成绩,用茎叶图表示如图:(Ⅰ)根据茎叶图中的数据完成下面的2×2列联表,并判断是否有95%的把握认为经常使用手机对学习成绩有影响?
| 及格(60及60以上) | 不及格 | 合计 | |
| 很少使用手机 | 20 | 7 | 27 |
| 经常使用手机 | 10 | 13 | 23 |
| 合计 | 30 | 20 | 50 |
参考公式及数据:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d
| P(K2≥k0) | 0.10 | 0.05 | 0.025 |
| k0 | 2.706 | 3.841 | 5.024 |
18.函数f(x)=$\left\{\begin{array}{l}{0,x∈\{0,4\}}\\{{x}^{2}-2x+3,0<x≤2}\\{|x-3|,2<x<4}\end{array}\right.$,若f(x)=kx有三个不同的根,则实数k的取值范围是( )
| A. | (0,$\frac{1}{4}$)∪(2$\sqrt{3}$-2,$\frac{3}{2}$] | B. | [0,$\frac{1}{4}$)∪(2$\sqrt{3}$-2,$\frac{3}{2}$] | C. | [0,$\frac{1}{4}$]∪(2$\sqrt{3}$-2,$\frac{3}{2}$] | D. | (0,$\frac{1}{4}$]∪(2$\sqrt{3}$-2,$\frac{3}{2}$] |
5.春节期间和谐小区从初一至初八连续8天举办大型文艺汇演,居民甲随机选择其中的连续3天观看演出,那么他在初一至初四期间连续3天看演出的概率为( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
2.设复数z1,z2在复平面内的对应点关于虚轴对称,z1=1+2i,i为虚数单位,则z1z2=( )
| A. | 1-2i | B. | 5i | C. | -5 | D. | 5 |
 ,则
,则 ”的否命题是( )
”的否命题是( )
 ,则
,则
 ,则
,则