题目内容
6.已知$\overrightarrow{AB}$=(5,-3),点A(3,1),则点B的坐标为( )| A. | (2,2) | B. | (-2,-2) | C. | (8,-2) | D. | (4,8) |
分析 设出B的坐标,利用向量直接列出方程求解即可.
解答 解:设B(x,y),$\overrightarrow{AB}$=(5,-3),点A(3,1),则(x-3,y-1)=(5,-3),
解得x=8,y=-2.
点B的坐标为(8,-2).
故选:C.
点评 本题考查向量相等,向量的基本计算,是基础题.

练习册系列答案
相关题目
16.已知数列{an}是递增的等比数列,a1+a4=9,a2a3=8,则数列{an}的前10项和等于( )
| A. | 1024 | B. | 1023 | C. | 512 | D. | 511 |
17.点A(sin1,cos1)在直角坐标平面上位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.设sinθ=$\frac{3}{5}$,cosθ=-$\frac{4}{5}$,则2θ的终边所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.矩形ABCD与矩形ABEF全等,且平面ABCD⊥平面ABEF,AD=2AB=2,若$\overrightarrow{FM}$=λ$\overrightarrow{FB}$,$\overrightarrow{AN}$=μ$\overrightarrow{AC}$,λ,μ∈R,λ+μ=1,则|$\overrightarrow{MN}$|的最小值为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{6}$ | D. | $\frac{\sqrt{6}}{3}$ |
16.下列函数中在($\frac{π}{4}$,$\frac{3}{4}$π)上为减函数的是( )
| A. | y=-tanx | B. | y=cos(2x-$\frac{π}{2}$) | C. | y=sin2x+cos2x | D. | y=2cos2x-1 |
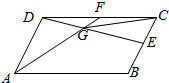 如图,已知E,F分别是平行四边形ABCD的边BC,CD中点,AF与DE相交于点G,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{GC}$=$\frac{3}{5}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示)
如图,已知E,F分别是平行四边形ABCD的边BC,CD中点,AF与DE相交于点G,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{GC}$=$\frac{3}{5}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示)