题目内容
15.矩形ABCD与矩形ABEF全等,且平面ABCD⊥平面ABEF,AD=2AB=2,若$\overrightarrow{FM}$=λ$\overrightarrow{FB}$,$\overrightarrow{AN}$=μ$\overrightarrow{AC}$,λ,μ∈R,λ+μ=1,则|$\overrightarrow{MN}$|的最小值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{6}$ | D. | $\frac{\sqrt{6}}{3}$ |
分析 建立空间坐标系,使用坐标表示出$\overrightarrow{MN}$,代入模长公式转化为求最小值问题.
解答  解:建立空间坐标系如图,则A(0,0,0),B(0,1,0),C(0,1,2),F(2,0,0),∴$\overrightarrow{AC}$=(0,1,2),$\overrightarrow{FB}$=(-2,1,0),
解:建立空间坐标系如图,则A(0,0,0),B(0,1,0),C(0,1,2),F(2,0,0),∴$\overrightarrow{AC}$=(0,1,2),$\overrightarrow{FB}$=(-2,1,0),
$\overrightarrow{FA}$=(-2,0,0)∴$\overrightarrow{AN}$=(0,μ,2μ),$\overrightarrow{FM}$=(-2λ,λ,0).∴$\overrightarrow{MN}$=-$\overrightarrow{FM}$+$\overrightarrow{FA}$+$\overrightarrow{AN}$=(2λ-2,μ-λ,2μ).
∴$\overrightarrow{MN}$2=(2λ-2)2+(μ-λ)2+(2μ)2=5λ2+5μ2-8λ-2λμ+4.∵λ+μ=1,∴λ=1-μ.
∴$\overrightarrow{MN}$2=5(1-μ)2+5μ2-8(1-μ)-2μ(1-μ)+4=12μ2-4μ+1=12(μ-$\frac{1}{6}$)2+$\frac{2}{3}$≥$\frac{2}{3}$.
∴当μ=$\frac{1}{6}$时,$\overrightarrow{MN}$2取得最小值$\frac{2}{3}$,∴|$\overrightarrow{MN}$|的最小值为$\sqrt{\frac{2}{3}}$=$\frac{\sqrt{6}}{3}$.
故选:D.
点评 本题考查了平面向量的线性运算及几何意义,结合图形表示出$\overrightarrow{MN}$是关键.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案| A. | (2,2) | B. | (-2,-2) | C. | (8,-2) | D. | (4,8) |
| A. | 不过点P且与l垂直的直线 | B. | 不过点P且与l平行的直线 | ||
| C. | 过点P且与l垂直的直线 | D. | 过点P且与l平行的直线 |
| A. | a>$\frac{1}{2}$ | B. | a<$\frac{1}{2}$ | C. | a≥$\frac{1}{2}$ | D. | a≤$\frac{1}{2}$ |
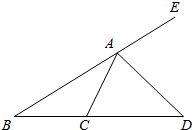 如图,AD是△ABC的外角∠EAC的平分线,那么$\frac{AB}{AC}$=$\frac{BD}{DC}$成立吗?
如图,AD是△ABC的外角∠EAC的平分线,那么$\frac{AB}{AC}$=$\frac{BD}{DC}$成立吗?