Question

1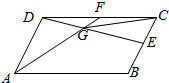．如图，已知E，F分别是平行四边形ABCD的边BC，CD中点，AF与DE相交于点G，若$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，则$\overrightarrow{GC}$=$\frac{3}{5}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}$（用$\overrightarrow{a}$，$\overrightarrow{b}$表示）

Answer 1

分析 设$\overrightarrow{AG}$=λ$\overrightarrow{AF}$，$\overrightarrow{DG}$=μ$\overrightarrow{DE}$，利用平面向量的基本定理解出λ，μ，再利用向量的三角形法则表示出$\overrightarrow{GC}$．

解答 解：$\overrightarrow{AF}$=$\overrightarrow{AD}+\overrightarrow{DF}$=$\frac{1}{2}\overrightarrow{a}+\overrightarrow{b}$，$\overrightarrow{DE}$=$\overrightarrow{DC}+\overrightarrow{CE}$=$\overrightarrow{a}-\frac{1}{2}\overrightarrow{b}$，
设$\overrightarrow{AG}$=λ$\overrightarrow{AF}$=$\frac{λ}{2}\overrightarrow{a}+λ\overrightarrow{b}$，$\overrightarrow{DG}$=μ$\overrightarrow{DE}$=$μ\overrightarrow{a}-\frac{μ}{2}\overrightarrow{b}$，则$\overrightarrow{AG}$=$\overrightarrow{AD}+\overrightarrow{DG}$=$\overrightarrow{b}$+$μ\overrightarrow{a}-\frac{μ}{2}\overrightarrow{b}$=$μ\overrightarrow{a}$+（1-$\frac{μ}{2}$）$\overrightarrow{b}$．
∴$\left\{\begin{array}{l}{\frac{λ}{2}=μ}\\{λ=1-\frac{μ}{2}}\end{array}\right.$，解得$\left\{\begin{array}{l}{λ=\frac{4}{5}}\\{μ=\frac{2}{5}}\end{array}\right.$．∴$\overrightarrow{GF}=\frac{1}{5}\overrightarrow{AF}$=$\frac{1}{10}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}$，∴$\overrightarrow{GC}=\overrightarrow{GF}+\overrightarrow{FC}$=$\frac{1}{10}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}$+$\frac{1}{2}\overrightarrow{a}$=$\frac{3}{5}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}$．
故答案为$\frac{3}{5}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}$．

点评 本题考查了平面向量的基本定理和几何意义，求出λ和μ是解题关键．