题目内容
18.设sinθ=$\frac{3}{5}$,cosθ=-$\frac{4}{5}$,则2θ的终边所在的象限是( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 由已知θ的正弦值和余弦值分别求出θ的范围,取交集后进一步得到2θ的范围.
解答 解:由sinθ=$\frac{3}{5}$$<\frac{\sqrt{2}}{2}$,得2kπ<θ<$\frac{π}{4}+2kπ$或$\frac{3π}{4}+2kπ<θ<π+2kπ$,k∈Z;
由cosθ=-$\frac{4}{5}$$<-\frac{\sqrt{2}}{2}$,得$\frac{3π}{4}+2kπ<θ<\frac{5π}{4}+2kπ$,k∈Z.
∴$\frac{3π}{4}+2kπ<θ<π+2kπ$,k∈Z.
则$\frac{3π}{2}+4kπ<2θ<2π+2kπ$,k∈Z.
∴2θ的终边所在的象限是第四象限.
故选:D.
点评 本题考查三角函数值的符号,体现了交集运算思想方法,是基础题.

练习册系列答案
相关题目
8.已知点P在椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1上,F1、F2为椭圆的两焦点,已知|PF1|=2,则|PF2|的值是( )
| A. | 1 | B. | 8 | C. | 3 | D. | 4 |
6.已知$\overrightarrow{AB}$=(5,-3),点A(3,1),则点B的坐标为( )
| A. | (2,2) | B. | (-2,-2) | C. | (8,-2) | D. | (4,8) |
7.已知点P(2,2)在直线l:Ax+By+C=0上,则方程Bx-Ay+4A+C=0是( )
| A. | 不过点P且与l垂直的直线 | B. | 不过点P且与l平行的直线 | ||
| C. | 过点P且与l垂直的直线 | D. | 过点P且与l平行的直线 |
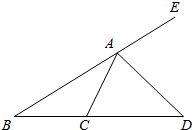 如图,AD是△ABC的外角∠EAC的平分线,那么$\frac{AB}{AC}$=$\frac{BD}{DC}$成立吗?
如图,AD是△ABC的外角∠EAC的平分线,那么$\frac{AB}{AC}$=$\frac{BD}{DC}$成立吗?