题目内容
已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的图象两相邻对称轴之间的距离是
,若将f(x)的图象先向右平移
个单位,所得函数g(x)为奇函数.
(1)求f(x)的解析式;
(2)求f(x)的单调区间.
| π |
| 2 |
| π |
| 6 |
(1)求f(x)的解析式;
(2)求f(x)的单调区间.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的图象
专题:三角函数的图像与性质
分析:(1)先求出ω=2,由所得函数g(x)为奇函数,可求得φ的值,从而确定f(x)的解析式;
(2)令2kπ+
≤2x+
≤2kπ+
,k∈z,解得x的范围,从而求得f(x)的单调减区间;令2kπ-
≤2x+
≤
+2kπ(k∈Z),从而求得f(x)的单调增区间.
(2)令2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
解答:
解:(1)由题意函数f(x)的图象两相邻对称轴之间的距离是
,可得函数的周期为π,即
=π,ω=2,故函数为f(x)=sin(2x+φ).
将函数f(x)图象向右平移
个单位,得到函数g(x)的解析式为 g(x)=sin[2(x-
)+φ]=sin(2x-
+φ),
∵函数g(x)为奇函数.
∴-
+φ=kπ,φ=kπ+
,k∈Z.
不妨令k=0,则φ取值为
.
故有f(x)=sin(ωx+φ)=sin(2x+
).
(2)因为函数y=sin(2x+
),
令2kπ-
≤2x+
≤
+2kπ k∈Z,即kπ-
≤x≤
+kπ(k∈Z),所以函数的单调增区间为:[kπ-
,
+kπ],k∈Z.
令2kπ+
≤2x+
≤2kπ+
,k∈z,求得kπ+
≤x≤kπ+
,k∈z,可求得函数的减区间为:[
+kπ,
+kπ],k∈Z.
| π |
| 2 |
| 2π |
| ω |
将函数f(x)图象向右平移
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
∵函数g(x)为奇函数.
∴-
| π |
| 3 |
| π |
| 3 |
不妨令k=0,则φ取值为
| π |
| 3 |
故有f(x)=sin(ωx+φ)=sin(2x+
| π |
| 3 |
(2)因为函数y=sin(2x+
| π |
| 3 |
令2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
| π |
| 12 |
| 5π |
| 12 |
| π |
| 12 |
令2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| π |
| 12 |
| 7π |
| 12 |
| π |
| 12 |
| 7π |
| 12 |
点评:本题主要考查了正弦函数的图象和单调性,考察了由y=Asin(ωx+φ)的部分图象确定其解析式,属于基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
点A、B、C、D在同一个球的球面上,且AB=CD=
,BC=2AC=2BD=2,则该球的表面积为( )
| 3 |
| A、16π | B、12π |
| C、8π | D、4π |
在△ABC中,已知角A,B,C所对的边分别为a,b,c,且a=3,c=8,B=60°,则△ABC的周长是( )
| A、17 | B、19 | C、16 | D、18 |
数列{an}的通项公式an=n2+2n,则数列{
}的前10项和为( )
| 1 |
| an |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图是2014年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,该数据的中位数和众数依次为( )
如图是2014年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,该数据的中位数和众数依次为( )| A、86,84 |
| B、84,84 |
| C、84,86 |
| D、85,86 |
 已知函数f(x)=x-
已知函数f(x)=x-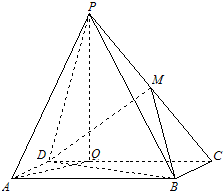 如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=4,AD=2,点P在底面的射影Q在CD上,且PQ=
如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=4,AD=2,点P在底面的射影Q在CD上,且PQ=