题目内容
函数f(x)=ax3+3x2+3x(a≠0).
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)若f(x)在区间(1,2)是增函数,求a的取值范围.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)若f(x)在区间(1,2)是增函数,求a的取值范围.
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)求出函数的导数,通过导数为0,利用二次函数的根,通过a的范围讨论f(x)的单调性;
(Ⅱ)当a>0,x>0时,f(x)在区间(1,2)是增函数,当a<0时,f(x)在区间(1,2)是增函数,推出f′(1)≥0且f′(2)≥0,即可求a的取值范围.
(Ⅱ)当a>0,x>0时,f(x)在区间(1,2)是增函数,当a<0时,f(x)在区间(1,2)是增函数,推出f′(1)≥0且f′(2)≥0,即可求a的取值范围.
解答:
解:(Ⅰ)函数f(x)=ax3+3x2+3x,
∴f′(x)=3ax2+6x+3,
令f′(x)=0,即3ax2+6x+3=0,则△=36(1-a),
①若a≥1时,则△≤0,f′(x)≥0,∴f(x)在R上是增函数;
②因为a≠0,∴当a≤1,△>0,f′(x)=0方程有两个根,x1=
,x2=
,
当0<a<1时,则当x∈(-∞,x2)或(x1,+∞)时,f′(x)>0,故函数在(-∞,x2)或(x1,+∞)是增函数;在(x2,x1)是减函数;
当a<0时,则当x∈(-∞,x1)或(x2,+∞),f′(x)<0,故函数在(-∞,x1)或(x2,+∞)是减函数;在(x1,x2)是增函数;
(Ⅱ)当a>0,x>0时,f′(x)=3ax2+6x+3>0 故a>0时,f(x)在区间(1,2)是增函数,
当a<0时,f(x)在区间(1,2)是增函数,
当且仅当:f′(1)≥0且f′(2)≥0,解得-
≤a<0,
a的取值范围[-
,0)∪(0,+∞).
∴f′(x)=3ax2+6x+3,
令f′(x)=0,即3ax2+6x+3=0,则△=36(1-a),
①若a≥1时,则△≤0,f′(x)≥0,∴f(x)在R上是增函数;
②因为a≠0,∴当a≤1,△>0,f′(x)=0方程有两个根,x1=
-1+
| ||
| a |
-1-
| ||
| a |
当0<a<1时,则当x∈(-∞,x2)或(x1,+∞)时,f′(x)>0,故函数在(-∞,x2)或(x1,+∞)是增函数;在(x2,x1)是减函数;
当a<0时,则当x∈(-∞,x1)或(x2,+∞),f′(x)<0,故函数在(-∞,x1)或(x2,+∞)是减函数;在(x1,x2)是增函数;
(Ⅱ)当a>0,x>0时,f′(x)=3ax2+6x+3>0 故a>0时,f(x)在区间(1,2)是增函数,
当a<0时,f(x)在区间(1,2)是增函数,
当且仅当:f′(1)≥0且f′(2)≥0,解得-
| 5 |
| 4 |
a的取值范围[-
| 5 |
| 4 |
点评:本题考查函数的导数的应用,判断函数的单调性以及已知单调性求解函数中的变量的范围,考查分类讨论思想的应用.

练习册系列答案
相关题目
设函数f(x)的定义域为D,若存在非零实数t使得对于任意x∈M(M⊆D),有x+t∈D,且f(x+t)≥f(x),则称f(x)为M上的“t高调函数”.如果定义域为R的函数f(x)是奇函数,当x≥0时,f(x)=|x-a2|-a2,且f(x)为R上的“4高调函数”,那么实数a的取值范围是( )
A、[-
| ||||||||
| B、[-1,1] | ||||||||
C、[-1,
| ||||||||
D、[-
|
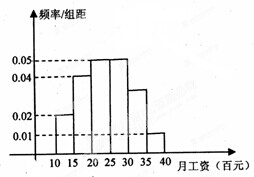 为了解工薪阶层的收入情况,某地政府调查了1000人的月工资收入,并把调查结果画成如图所示的频率分布直方图,则由图知月工资在(30,35](百元)的人数为( )
为了解工薪阶层的收入情况,某地政府调查了1000人的月工资收入,并把调查结果画成如图所示的频率分布直方图,则由图知月工资在(30,35](百元)的人数为( )| A、80 | B、150 |
| C、230 | D、400 |
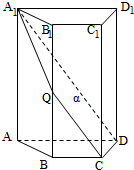 如图,四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC,过A1、C、D三点的平面记为α,BB1与α的交点为Q.
如图,四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC,过A1、C、D三点的平面记为α,BB1与α的交点为Q.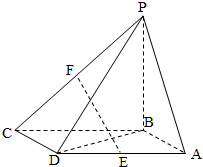 如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD=
如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD= 一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.