题目内容
函数y=
+2
的最小值为（ ）
| x+1 |
| x-1 |
| A、1 | ||
B、
| ||
| C、2 | ||
| D、0 |
考点：函数的最值及其几何意义
专题：计算题,函数的性质及应用
分析：确定函数的定义域为[1，+∞），函数y=
+2
在[1，+∞）上单调递增，即可求出函数y=
+2
的最小值．
| x+1 |
| x-1 |
| x+1 |
| x-1 |
解答：
解：由题意，函数的定义域为[1，+∞）．
∵函数y=
+2
在[1，+∞）上单调递增，
∴函数y=
+2
的最小值为
，
故选B．
∵函数y=
| x+1 |
| x-1 |
∴函数y=
| x+1 |
| x-1 |
| 2 |
故选B．
点评：本题考查函数的最值及其几何意义，考查函数的单调性，考查学生分析解决问题的能力，比较基础．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
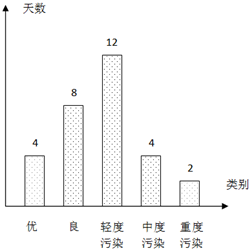经过对某市空气质量指数进行一个月（30天）监测，获得数据后得到条形图统计图：