题目内容
对于函数f(x),若存在区间M=[a,b](其中a<b),使得{y|y=f(x),x∈M}=[2a,2b],则称区间M为函数f(x)的一个“增值区间”.给出下列4个函数:
①f(x)=x2-2x+4;
②f(x)=|2x-1|;
③f(x)=ex-1;
④f(x)=ln(x+1).
其中存在“增值区间”的函数有 (填出所有满足条件的函数序号).
①f(x)=x2-2x+4;
②f(x)=|2x-1|;
③f(x)=ex-1;
④f(x)=ln(x+1).
其中存在“增值区间”的函数有
考点:函数单调性的判断与证明
专题:阅读型,方程思想,函数的性质及应用
分析:根据题意可得出:存在“增值区间”的函数,必须满足f(x)=2x有2个不等实数根,即f(x)与g(x)=2x有2个不同的交点,运用图象判断即可.
解答:
解:∵于函数f(x),若存在区间M=[a,b](其中a<b),使得{y|y=f(x),x∈M}=[2a,2b],则称区间M为函数f(x)的一个“增值区间”.
∴f(x)=2x,有2个不等实数根,
①f(x)=x2-2x+4=2x,
x2-4x+4=0,
x=2,b不符合题意,
∴①不是增值区间函数,
∵②f(x)=|2x-1|;与g(x)=2x
∴|2x-1|=2x有2个不等实根,
f(x)=|2x-1|;与g(x)=2x有2个不同的交点,
据图说明②符合题意,是增值区间函数.
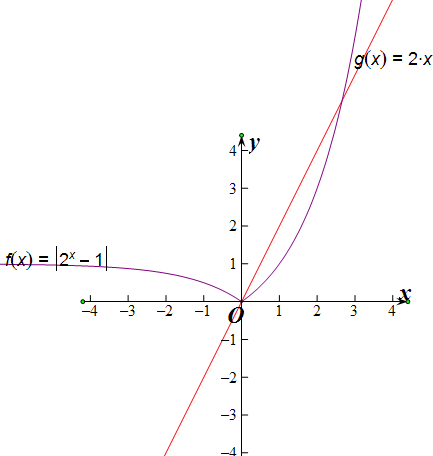
③f(x)=ex-1;
f(x)=ex-1;与g(x)=2x∴③是增值区间函数.
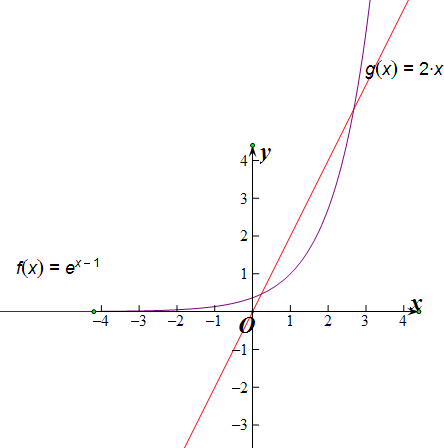
④f(x)=ln(x+1).与g(x)=2x,
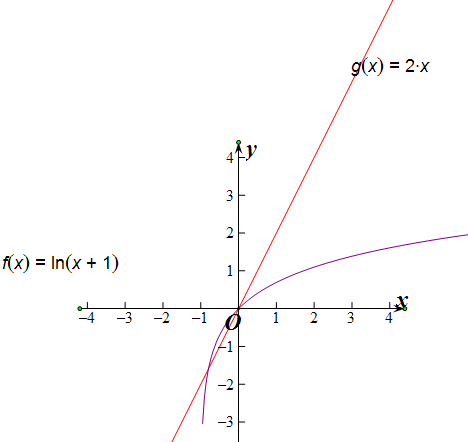
ln(x+1)=2x有2个不等实根,
f(x)=ln(x+1).与g(x)=2x有2个不同的交点,
∴④是增值区间函数.
故答案为:②③④
∴f(x)=2x,有2个不等实数根,
①f(x)=x2-2x+4=2x,
x2-4x+4=0,
x=2,b不符合题意,
∴①不是增值区间函数,
∵②f(x)=|2x-1|;与g(x)=2x
∴|2x-1|=2x有2个不等实根,
f(x)=|2x-1|;与g(x)=2x有2个不同的交点,
据图说明②符合题意,是增值区间函数.

③f(x)=ex-1;
f(x)=ex-1;与g(x)=2x∴③是增值区间函数.

④f(x)=ln(x+1).与g(x)=2x,
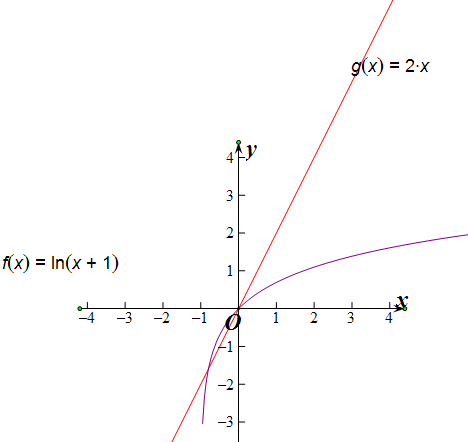
ln(x+1)=2x有2个不等实根,
f(x)=ln(x+1).与g(x)=2x有2个不同的交点,
∴④是增值区间函数.
故答案为:②③④
点评:本题考查了运用方程的解判断增值区间函数,转化为函数图象的交点问题求解,画出函数图象,根据图象判断,属于数形结合的思想解决问题,关键是理解题意.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
函数y=
+2
的最小值为( )
| x+1 |
| x-1 |
| A、1 | ||
B、
| ||
| C、2 | ||
| D、0 |
曲线的极坐标方程ρ=4sinθ化为直角坐标为( )
| A、x2+(y+2)2=4 |
| B、x2+(y-2)2=4 |
| C、(x-2)2+y2=4 |
| D、(x+2)2+y2=4 |
一个空间几何体的三视图如图所示,则该几何体的表面积为( )


| A、48 | ||
B、32+8
| ||
C、48+8
| ||
| D、80 |
正四棱锥(顶点在底面的射影是底面正方形的中心)的体积为12,底面对角线的长为2
,则侧面与底面所成的二面角为( )
| 6 |
| A、30° | B、45° |
| C、60° | D、90° |
已知m,n是两条不同直线,α,β,γ是三个不同平面,下列命题中正确的是( )
| A、若m⊥α,n⊥m则n∥α |
| B、若α⊥β,β⊥γ则α∥β |
| C、若m⊥β,n⊥β则m∥n |
| D、若m∥α,m∥β,则α∥β |