题目内容
解不等式：|x+3|＞|x-5|+7．
考点：其他不等式的解法
专题：不等式
分析：将不等式转化为不等式组，即可得到结论．
解答：
解：①若x＜-3，则不等式等价为-（x+3）＞-（x-5）+7，
即-3＞7，此时不等式无解；
②若-3≤x≤5，则不等式等价为x+3＞-（x-5）+7，
即x＞
，此时
＜x≤5；
③若x＞5，则不等式等价为x+3＞x-5+7，
即3＞2，此时x＞5．
综上：x＞
，
即不等式的解集为（
，+∞）．
即-3＞7，此时不等式无解；
②若-3≤x≤5，则不等式等价为x+3＞-（x-5）+7，
即x＞
| 9 |
| 2 |
| 9 |
| 2 |
③若x＞5，则不等式等价为x+3＞x-5+7，
即3＞2，此时x＞5．
综上：x＞
| 9 |
| 2 |
即不等式的解集为（
| 9 |
| 2 |
点评：本题主要考查不等式的解法，利用绝对值不等式的性质，进行分类讨论是解决本题的关键．
练习册系列答案
相关题目
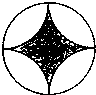如图，将半径为l的圆分成相等的四段弧，再将四段弧围成星形放在圆内（阴影部分）．现在往圆内任投一点，此点落在星形区域内的概率为（ ）A、
| ||||
B、
| ||||
C、1-
| ||||
D、
|
已知函数f（x）=sin（
-x），若要得到函数f′（x）的图象，只需将函数y=f（x）图象上所有的点（ ）
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
