题目内容
有5名同学一起旅游,
(1)在某景点留影,4个人站成一排,余下一人摄影,如果只有甲不会摄影则有多少种不同的排法?
(2)在某湖区乘快艇游览,每只快艇最多只能容纳4人,因此这5人要分成两组,则有多少种不同的分法?
(1)在某景点留影,4个人站成一排,余下一人摄影,如果只有甲不会摄影则有多少种不同的排法?
(2)在某湖区乘快艇游览,每只快艇最多只能容纳4人,因此这5人要分成两组,则有多少种不同的分法?
考点:排列、组合的实际应用
专题:计算题
分析:(1)根据题意,分2步进行分析:先在其余4人种选1人照相,再将剩余的4人全排列,分别求出其排法数目,进而由分步计数原理计算可得答案;
(2)首先分析5人分成2组分别对应2只快艇的分组方法数目,进而由组合数公式计算每种分组方法的情况数目,由分类加法原理计算可得答案.
(2)首先分析5人分成2组分别对应2只快艇的分组方法数目,进而由组合数公式计算每种分组方法的情况数目,由分类加法原理计算可得答案.
解答:
解:(1)根据题意,分2步进行分析:
①、先在其余4人种选1人照相,有C41=4种排法,
②、再将剩余的4人全排列,有A44=24种,
则共有4×24=96种排法.
(2)根据题意,5人分成2组分别对应2只快艇,
一组最多4人,最少1人,有1、4,2、3,3、2,4、1;共4种分组方法;
即有C51+C52+C53+C54=30种分法.
①、先在其余4人种选1人照相,有C41=4种排法,
②、再将剩余的4人全排列,有A44=24种,
则共有4×24=96种排法.
(2)根据题意,5人分成2组分别对应2只快艇,
一组最多4人,最少1人,有1、4,2、3,3、2,4、1;共4种分组方法;
即有C51+C52+C53+C54=30种分法.
点评:本题考查排列、组合的应用,关键是正确运用分步、分类原理进行分析,结合组合、排列公式进行计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
复数z=
(i是虚数单位)的共轭复数
在复平面内对应的点在( )
| i |
| 1-i |
. |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知m≥2,点P(x,y)满足
点Q的坐标为(0,-1),记f(m)为
•
的最小值,则f(m)的最大值为( )
|
| OP |
| OQ |
A、-
| ||
B、-
| ||
| C、0 | ||
D、
|
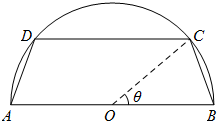 一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分.现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD(如图所示,其中O为圆心,C,D在半圆上),设∠BOC=θ,木梁的体积为V(单位:m3),表面积为S(单位:m2).
一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分.现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD(如图所示,其中O为圆心,C,D在半圆上),设∠BOC=θ,木梁的体积为V(单位:m3),表面积为S(单位:m2).