题目内容
19.某几何体的三视图如图所示,则该几何体中最长的棱长为( )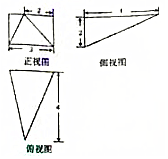
| A. | $3\sqrt{3}$ | B. | $2\sqrt{6}$ | C. | $\sqrt{21}$ | D. | $2\sqrt{5}$ |
分析 如图所示,该几何体为四棱锥P-ABCD.侧面PAB⊥底面ABCD,底面ABCD为矩形,过点P作PE⊥AB,垂足为点E,AE=1,BE=2,AD=2,PE=4.
解答 解:如图所示,该几何体为四棱锥P-ABCD.
侧面PAB⊥底面ABCD,底面ABCD为矩形,过点P作PE⊥AB,垂足为点E,AE=1,BE=2,AD=2,PE=4.
该几何体中最长的棱长为PC=$\sqrt{{4}^{2}+{2}^{2}+{2}^{2}}$=2$\sqrt{6}$.
故选:B.
点评 本题考查了长方体与四棱锥的三视图、勾股定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
10.执行如图所示的程序框图,若输入n=5,则输出的S值为( )
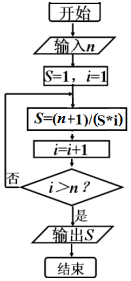

| A. | $\frac{1}{20}$ | B. | $\frac{5}{16}$ | C. | $\frac{16}{5}$ | D. | $\frac{3}{8}$ |
7.已知两点A(-m,0)和B(2+m,0)(m>0),若在直线l:x+$\sqrt{3}$y-9=0上存在点P,使得PA⊥PB,则实数m的取值范围是( )
| A. | (0,3) | B. | (0,4) | C. | [3,+∞) | D. | [4,+∞) |
14.在极坐标系中,曲线C:sinθ=|cosθ|上不同的两点M,N到直线l:ρcosθ-2ρsinθ=2的距离为$\sqrt{5}$,则|MN|=( )
| A. | $2\sqrt{5}$ | B. | $4\sqrt{5}$ | C. | 8 | D. | 16 |