题目内容
18.在三棱锥P-ABC中,PA=$\sqrt{2}$,PB=$\sqrt{3}$,PC=2,且PA,PB,PC两两垂直,则此三棱锥外接球的体积是$\frac{9π}{2}$.分析 三棱锥扩展为长方体,然后求解外接球的半径,求解体积即可.
解答 解:在三棱锥P-ABC中,PA=$\sqrt{2}$,PB=$\sqrt{3}$,PC=2,且PA,PB,PC两两垂直,
三棱锥扩展为长方体,长方体的对角线的长度就是外接球的直径,
三棱锥P-ABC外接球的半径为$\frac{1}{2}\sqrt{{{(\sqrt{2})}^2}+{{(\sqrt{3})}^2}+{2^2}}=\frac{3}{2}$,
所以其外接球的体积为$\frac{4}{3}π{(\frac{3}{2})^3}=\frac{9π}{2}$.
故答案为:$\frac{9π}{2}$.
点评 本题考查几何体的外接球的体积的求法,考查空间想象能力以及计算能力.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
8.若集合A={x|x2+2x-8<0},集合B={x|-2<x<4},则A∩B等于( )
| A. | ∅ | B. | (-2,3) | C. | (-2,4) | D. | (-2,2) |
10.执行如图所示的程序框图,若输入n=5,则输出的S值为( )
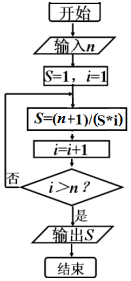

| A. | $\frac{1}{20}$ | B. | $\frac{5}{16}$ | C. | $\frac{16}{5}$ | D. | $\frac{3}{8}$ |
7.已知两点A(-m,0)和B(2+m,0)(m>0),若在直线l:x+$\sqrt{3}$y-9=0上存在点P,使得PA⊥PB,则实数m的取值范围是( )
| A. | (0,3) | B. | (0,4) | C. | [3,+∞) | D. | [4,+∞) |