Question

3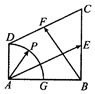．在直角梯形ABCD中，AB⊥AD，AD∥BC，AB=BC=2AD=2，E，F分别为BC，CD的中点，以A为圆心，AD为半径的圆交AB于G，点P在$\widehat{DG}$上运动（如图）．若$\overrightarrow{AP}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{BF}$，其中λ，μ∈R，则6λ+μ的取值范围是（　　）

• A． [1，$\sqrt{2}$]
• B． [$\sqrt{2}$，2$\sqrt{2}$]
• C． [2，2$\sqrt{2}$]
• D． [1，2$\sqrt{2}$]

Answer 1

分析 建立如图所示的坐标系，则A（0，0），B（2，0），D（0，1），C（2，2），E（2，1），F（1，1.5），P（cosα，sinα）（0≤α≤$\frac{π}{2}$），
由$\overrightarrow{AP}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{BF}$得，（cosα，sinα）=λ（2，1）+μ（-1，$\frac{3}{2}$），λ，μ用参数α进行表示，利用辅助角公式化简，即可得出结论．

解答 解：建立如图所示的坐标系，
则A（0，0），B（2，0），D（0，1），C（2，2），E（2，1），F（1，1.5），
P（cosα，sinα）（0≤α≤$\frac{π}{2}$），
由$\overrightarrow{AP}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{BF}$得，（cosα，sinα）=λ（2，1）+μ（-1，$\frac{3}{2}$）
⇒cosα=2λ-μ，sinα=λ+$\frac{3}{2}μ$
⇒λ=$\frac{3}{8}cosα+\frac{1}{4}sinα$，$μ=\frac{1}{2}sinα-\frac{1}{4}cosα$
∴6λ+μ=6（$\frac{3}{8}cosα+\frac{1}{4}sinα$）+$\frac{1}{2}sinα-\frac{1}{4}cosα$=2（sinα+cosα）=2$\sqrt{2}$sin（$α+\frac{π}{4}$）
∵$α+\frac{π}{4}∈[\frac{π}{4}，\frac{3π}{4}]$，∴sin（$α+\frac{π}{4}$）$∈[\frac{\sqrt{2}}{2}，1]$
∴2$\sqrt{2}$sin（$α+\frac{π}{4}$）∈[2，2$\sqrt{2}$]，即6λ+μ的取值范围是[2，2$\sqrt{2}$]．
故选：C

点评 本题考查平面向量的坐标运算，考查学生的计算能力，正确利用坐标系是关键．属于中档题．