题目内容
6.函数f(x)=$\frac{6x}{{1+{x^2}}}$在区间[0,3]的最大值为( )| A. | 3 | B. | 4 | C. | 2 | D. | 5 |
分析 利用基本不等式求解表达式的最大值即可.
解答 解:当x≠0时,
函数f(x)=$\frac{6x}{{1+{x^2}}}$=$\frac{6}{\frac{1}{x}+x}$≤$\frac{6}{2\sqrt{x•\frac{1}{x}}}$=3,当且仅当x=1时,函数取得最大值3.
x=1∈[0,3],成立.
故选:A.
点评 本题考查基本不等式在最值中的应用,考查计算能力.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
14.下列表述正确的是( )
①归纳推理是由特殊到一般的推理;
②演绎推理是由一般到特殊的推理;
③类比推理是由特殊到一般的推理;
④分析法是一种间接证明法.
①归纳推理是由特殊到一般的推理;
②演绎推理是由一般到特殊的推理;
③类比推理是由特殊到一般的推理;
④分析法是一种间接证明法.
| A. | ①②③④ | B. | ②③④ | C. | ①②④ | D. | ①② |
1.已知棱长为2,各面均为等边三角形的四面体S-ABC的各顶点都在球O的球面上,则球O的表面积为( )
| A. | π | B. | 2π | C. | 4π | D. | 6π |
11.某产品的广告费用x与销售额y的统计数据如表:
根据上表可得回归方程$\hat y=9.4x+9.1$,据此模型预报广告费用为6万元时,销售额为( )
| 广告费用x(万元) | 4 | 2 | 3 | 5 |
| 销售额y(万元) | 49 | 26 | 39 | 54 |
| A. | 72.0万元 | B. | 67.7万元 | C. | 65.5万元 | D. | 63.6万元 |
18. 如图,已知点D为三角形ABC边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N*)为AC边上的一列点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-(3an+2)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中,an>0,a1=1,则{an}的通项公式为( )
如图,已知点D为三角形ABC边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N*)为AC边上的一列点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-(3an+2)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中,an>0,a1=1,则{an}的通项公式为( )
 如图,已知点D为三角形ABC边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N*)为AC边上的一列点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-(3an+2)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中,an>0,a1=1,则{an}的通项公式为( )
如图,已知点D为三角形ABC边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N*)为AC边上的一列点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-(3an+2)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中,an>0,a1=1,则{an}的通项公式为( )| A. | 3•2n-1-1 | B. | 2n-1 | C. | 3n-2 | D. | 2•3n-1-1 |
15.观察下列各式:55=3 125,56=15 625,57=78 125,…,则52017的末四位数字为( )
| A. | 3 125 | B. | 5 625 | C. | 8 125 | D. | 0 625 |
2.如图给出的是计算$1+\frac{1}{3}+\frac{1}{5}++\frac{1}{119}$的值的一个程序框图,其中判断框内可以填入的条件是( )
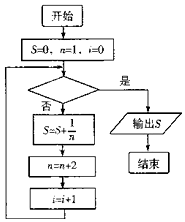

| A. | i≤119? | B. | i≥119? | C. | i≤60? | D. | i≥60? |