题目内容
12.已知定义在R上的函数f(x)满足f(x+5)=f(x-5),且0≤x≤5时,f(x)=4-x,则f(1003)=( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 根据条件判断函数的周期性,利用函数的周期进行求解即可.
解答 解:∵f(x+5)=f(x-5),
∴f(x+10)=f(x),则函数f(x)是周期为10的周期函数,
则f(1003)=f(1000+3)=f(3)=4-3=1,
故选:C.
点评 本题主要考查函数值的计算,利用函数周期性的性质进行转化是解决本题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
3.下列说法正确的是( )
| A. | 命题“若a>b,则a2>b2”的否命题是“若a<b,则a2<b2” | |
| B. | 命题“若a>b,则a2>b2”的逆命题是“若a≤b,则a2≤b2” | |
| C. | 命题“?x∈R,cosx<1”的否定命题是“?x0∈R,cosx0≥1” | |
| D. | 命题“?x∈R,cosx<1”的否定命题是“?x0∈R,cosx0>1” |
17.某学校高中毕业班有男生900人,女生600人,学校为了对高三学生数学学习情况进行分析,从高三年级按照性别进行分层抽样,抽取200名学生成绩,统计数据如表所示:
(Ⅰ)若成绩90分以上(含90分),则成绩为及格,请估计该校毕业班平均成绩及格学生人数;
(Ⅱ)如果样本数据中,有60名女生数学成绩合格,请完成如下数学成绩与性别的列联表,并判断是否有90%的把握认为“该校学生的数学成绩与性别有关”.
参考公式:K2=$\frac{n(ad-bc)^2}{(a+b)(c+d)(a+c)(b+d)}$.
| 分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150) | 总计 |
| 频数 | 20 | 40 | 70 | 50 | 20 | 200 |
(Ⅱ)如果样本数据中,有60名女生数学成绩合格,请完成如下数学成绩与性别的列联表,并判断是否有90%的把握认为“该校学生的数学成绩与性别有关”.
| 女生 | 男生 | 总计 | |
| 及格人数 | 60 | ||
| 不及格人数 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
4.设函数f(x)=sinωx(ω>0),将f(x)的图象向左平移$\frac{π}{6}$个单位长度后,所得的图象与y=cosωx的图象重合,则ω的最小值等于( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | 6 | D. | 9 |
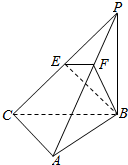 如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,M为AB的中点,点F在PA上,且2PF=FA.
如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,M为AB的中点,点F在PA上,且2PF=FA.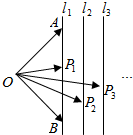 如图,已知l1,l2,l3,…ln为平面内相邻两直线距离为1的一组平行线,点O到l1的距离为2,A,B是l1的上的不同两点,点P1,P2,P3,…Pn分别在直线l1,l2,l3,…ln上.若$\overrightarrow{O{P}_{n}}$=xn$\overrightarrow{OA}$+yn$\overrightarrow{OB}$(n∈N*),则x1+x2+…+x5+y1+y2+…+y5的值为10.
如图,已知l1,l2,l3,…ln为平面内相邻两直线距离为1的一组平行线,点O到l1的距离为2,A,B是l1的上的不同两点,点P1,P2,P3,…Pn分别在直线l1,l2,l3,…ln上.若$\overrightarrow{O{P}_{n}}$=xn$\overrightarrow{OA}$+yn$\overrightarrow{OB}$(n∈N*),则x1+x2+…+x5+y1+y2+…+y5的值为10.