题目内容
7.设常数λ>0,a>0,函数f(x)=$\frac{{x}^{2}}{λ+x}$-alnx.(1)当a=$\frac{3}{4}$λ时,若f(x)最小值为0,求λ的值;
(2)对任意给定的正实数λ,a,证明:存在实数x0,当x>x0时,f(x)>0.
分析 (1)当a=$\frac{3}{4}$λ时,函数f(x)=$\frac{{x}^{2}}{λ+x}$-$\frac{3}{4}λlnx$(x>0).f′(x)=$\frac{(x-λ)(4{x}^{2}+9λx+3{λ}^{2})}{4x(λ+x)^{2}}$,分别解出f′(x)>0,f′(x)<0,研究其单调性,即可得出最小值.
(2)函数f(x)=x-$λ+\frac{{λ}^{2}}{λ+x}$-alnx>x-λ-alnx.令u(x)=x-λ-alnx.利用导数研究其单调性即可得出.
解答 (1)解:当a=$\frac{3}{4}$λ时,函数f(x)=$\frac{{x}^{2}}{λ+x}$-alnx=$\frac{{x}^{2}}{λ+x}$-$\frac{3}{4}λlnx$(x>0).
f′(x)=$\frac{x(2λ+x)}{(λ+x)^{2}}$-$\frac{3λ}{4x}$=$\frac{(x-λ)(4{x}^{2}+9λx+3{λ}^{2})}{4x(λ+x)^{2}}$,
∵λ>0,x>0,∴4x2+9λx+3λ2>0,4x(λ+x)2>0.
∴当x>λ时,f′(x)>0,此时函数f(x)单调递增;
当0<x<λ时,f′(x)<0,此时函数f(x)单调递减.
∴当x=λ时,函数f(x)取得极小值,即最小值,
∴f((λ)=$\frac{{λ}^{2}}{2λ}-$$\frac{3λ}{4}lnλ$=0,解得λ=${e}^{\frac{2}{3}}$.
(2)证明:函数f(x)=$\frac{{x}^{2}}{λ+x}$-alnx=$\frac{{x}^{2}-{λ}^{2}+{λ}^{2}}{λ+x}$-alnx=x-$λ+\frac{{λ}^{2}}{λ+x}$-alnx>x-λ-alnx.
令u(x)=x-λ-alnx.
u′(x)=1-$\frac{a}{x}$=$\frac{x-a}{x}$,可知:当x>a时,u′(x)>0,函数u(x)单调递增,x→+∞,u(x)→+∞.
一定存在x0>0,使得当x>x0时,u(x0)>0,
∴存在实数x0,当x>x0时,f(x)>u(x)>u(x0)>0.
点评 本题考查了利用导数研究函数的单调性极值与最值、分类讨论方法、恒成立问题的等价转化方法,考查了推理能力与计算能力,属于难题.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案| A. | an+1-a | B. | n(a+1) | C. | na | D. | (a+1)n-1 |
| A. | y=sinx | B. | y=-|x+1| | C. | $y=ln\frac{2-x}{2+x}$ | D. | y=$\frac{1}{2}$(2x+2-x) |
| A. | (-∞,-2) | B. | (-2,0) | C. | (0,1) | D. | (1,+∞) |
| A. | $\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{20}$=1 | ||
| C. | $\frac{3{x}^{2}}{25}$-$\frac{3{y}^{2}}{100}$=1 | D. | $\frac{3{x}^{2}}{100}$-$\frac{3{y}^{2}}{25}$=1 |

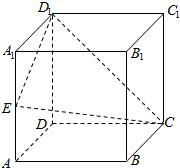 如图,有一个正方体的木块,E为棱AA1的中点.现因实际需要,需要将其沿平面D1EC将木块锯开.请你画出前面ABB1A1与截面D1EC的交线,并说明理由.
如图,有一个正方体的木块,E为棱AA1的中点.现因实际需要,需要将其沿平面D1EC将木块锯开.请你画出前面ABB1A1与截面D1EC的交线,并说明理由.