题目内容
下列命题错误的是( )
| A、“x=1”是“x2-3x+2=0”的充分不必要条件 |
| B、对于命题p:?x∈R,使得x2+x+1<0;则?p:?x∈R,均有x2+x+1≥0 |
| C、命题“若m>0,则方程x2+x-m=0有实根”的逆否命题为“若方程x2+x-m=0无实根,则m≤0” |
| D、命题“若xy=0,则x、y中至少有一个为零”的否定式“若xy≠0,则x、y都不为零” |
考点:命题的真假判断与应用
专题:简易逻辑
分析:A.“x=1”⇒“x2-3x+2=0”,反之不成立,即可判断出;
B.利用¬P的意义即可得出;
C利用逆否命题的定义即可得出;
D.利用“非命题”的意义即可得出.
B.利用¬P的意义即可得出;
C利用逆否命题的定义即可得出;
D.利用“非命题”的意义即可得出.
解答:
解:A.“x=1”⇒“x2-3x+2=0”,反之不成立,因此“x=1”是“x2-3x+2=0”的充分不必要条件,正确;
B.命题p:?x∈R,使得x2+x+1<0;可得?p:?x∈R,均有x2+x+1≥0,正确;
C.“若m>0,则方程x2+x-m=0有实根”的逆否命题为“若方程x2+x-m=0无实根,则m≤0”正确;
D.命题“若xy=0,则x、y中至少有一个为零”的否定应为“若xy=0,则x、y都不为零”,因此D不正确.
综上可知:只有D不正确.
故选:D.
B.命题p:?x∈R,使得x2+x+1<0;可得?p:?x∈R,均有x2+x+1≥0,正确;
C.“若m>0,则方程x2+x-m=0有实根”的逆否命题为“若方程x2+x-m=0无实根,则m≤0”正确;
D.命题“若xy=0,则x、y中至少有一个为零”的否定应为“若xy=0,则x、y都不为零”,因此D不正确.
综上可知:只有D不正确.
故选:D.
点评:本题考查了简易逻辑的有关知识,属于基础题.

练习册系列答案
相关题目
已知变量x,y满足约束条件
,则z=x+2y的最大值为( )
|
| A、6 | B、5 | C、4 | D、3 |
若双曲线
-x2=1的渐近线方程为y=±
x,则双曲线离心率为( )
| y2 |
| m2 |
| 2 |
A、
| ||||
| B、3 | ||||
C、
| ||||
D、
|
圆C:x2+y2-2x=0的圆心到双曲线x2-
2=1的渐近线的距离是( )
| y |
| 3 |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
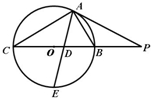 如图所示,PA为圆O的切线,A为切点,PO交圆O于B,C两点,PA=20,PB=10,∠BAC的角平分线与BC和圆O分别交于点D和E.
如图所示,PA为圆O的切线,A为切点,PO交圆O于B,C两点,PA=20,PB=10,∠BAC的角平分线与BC和圆O分别交于点D和E. 如图,已知△ABC内接于圆O,点D在OC的延长线上,AD是⊙O的切线,若∠B=30°,AC=3,则OD的长为
如图,已知△ABC内接于圆O,点D在OC的延长线上,AD是⊙O的切线,若∠B=30°,AC=3,则OD的长为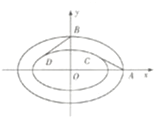 如图,内外两个椭圆的离心率相同,从外层椭圆顶点向内层椭圆引切线AC,BD,设内层椭圆方程为
如图,内外两个椭圆的离心率相同,从外层椭圆顶点向内层椭圆引切线AC,BD,设内层椭圆方程为