题目内容
已知数列{an}满足:
+
+
+…+
=n2(n∈N*),令bn=anan+1,Sn为数列{bn}的前n项和.
(1)求an和Sn;
(2)对任意的正整数n,不等式Sn>λ-
恒成立,求实数λ的取值范围.
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
(1)求an和Sn;
(2)对任意的正整数n,不等式Sn>λ-
| 1 |
| 2 |
考点:数列与不等式的综合
专题:计算题,点列、递归数列与数学归纳法
分析:(1)先求出首项,再将n换成n-1,两式相减即可得到通项,再由裂项相消求和得到前n项的和;
(2)运用参数分离,根据数列{Sn}是单调递增数列,即可求出前n项和的最小值,从而得到实数λ的取值范围.
(2)运用参数分离,根据数列{Sn}是单调递增数列,即可求出前n项和的最小值,从而得到实数λ的取值范围.
解答:
解:(1)由于
+
+
+…+
=n2(n∈N*),①
当n=1时,a1=1;
当n≥2时,
+
+
+…+
=(n-1)2,②
则①-②得
=2n-1,即an=
,
综上,an=
,n∈N*;
bn=
=
(
-
),
则Sn=
[(1-
)+(
-
)+…+(
-
)],
则Sn=
(1-
).
(2)由Sn>λ-
得λ<Sn+
,
所以λ<(Sn+
)min,
因为{Sn}是单调递增数列,所以当n=1时Sn取得最小值为
,
因此λ<
.
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
当n=1时,a1=1;
当n≥2时,
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an-1 |
则①-②得
| 1 |
| an |
| 1 |
| 2n-1 |
综上,an=
| 1 |
| 2n-1 |
bn=
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
则Sn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
则Sn=
| 1 |
| 2 |
| 1 |
| 2n+1 |
(2)由Sn>λ-
| 1 |
| 2 |
| 1 |
| 2 |
所以λ<(Sn+
| 1 |
| 2 |
因为{Sn}是单调递增数列,所以当n=1时Sn取得最小值为
| 1 |
| 3 |
因此λ<
| 5 |
| 6 |
点评:本题考查数列的通项和前n项和的求法,注意将下标变换相减法和裂项相消求和,同时考查不等式的恒成立问题转化为求数列的最值问题,属于中档题.

练习册系列答案
相关题目
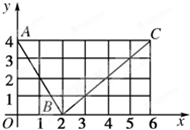 如图所示折线段ABC,其中A、B、C的坐标分别为(0,4),(2,0),(6,4).
如图所示折线段ABC,其中A、B、C的坐标分别为(0,4),(2,0),(6,4).